Inéquation avec valeurs absolues

[waterloo]

Bonjour à tous!

Je voulais voir avec vous une inéquation avec des valeurs absolues.

I 4 - x^2 I - I3 - x I > x j'obtiens S= ] -racine(7); 3 ]

Je suis parti en faisant un tableau de - infini -2 2 3 +infini pour I 4 - x^2 I - I3 - x I
au cour duquel j'obtiens 4 polynomes de 2nd degré. Et je dois trouver les valeurs de x pour que les 4 polynomes soient superieurs à x c'est à dire: polynome - x > 0 .
J'obtiens S1 S2 S3 S4 et je fais l'intersection des 4 S pour obtenir S= ] -racine(7); 3 ].


Je vous remercie par avance pour les réponses que vous m'allait m'apporter sur mon raisonnement et la réponse

[mathelot]

Je vous remercie par avance pour les réponses que vous allez m'apporter sur mon raisonnement et la réponse

bonjour,
il faut considérer la réunion des quatre intervalles de solutions:



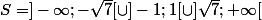
pourquoi est ce la réunion ? parce que la variable x peut vérifier une condition ou l'autre.
Si en français, on connecte les propriétés par un ou, on connecte les ensembles par une réunion

La réunion se code \cup en MimeTex entouré des balises tex et /tex

[Black Jack]

Bonjour mathelot,

Peux-tu m'expliquer pourquoi tu as exclu la valeur 3 dans les solutions ?

Avec x = 3, on a :

I 4 - x^2 I - I3 - x I > x
I 4 - 9 I - I3 - 3I > 3
5 > 3

[mathelot]

Bonjour mathelot,

Peux-tu m'expliquer pourquoi tu as exclu la valeur 3 dans les solutions ?

Avec x = 3, on a :

I 4 - x^2 I - I3 - x I > x
I 4 - 9 I - I3 - 3I > 3
5 > 3

C'est une erreur. Merci de l'avoir corrigée. Je fais la correction.

[waterloo]

Oui dans ce cas là ca donne S= ]-infini;-racine(7)[U]-1;1[U]1-racine(2);1+racine(2)[U]racine(7);infini[


mais la ou je ne comprends pas c'est par exemple pour ]-infini ; -2[ ,
nous obtenons S1=]-infini;-racine(7)[U]racine(7);infini[ . Or les valeurs de x appartiennent que pour ]-infini;-racine(7)[ donc S1 est vrai que pour ]-infini;-racine(7)[ ?

[mathelot]

Oui dans ce cas là ca donne S= ]-infini;-racine(7)[U]-1;1[U]1-racine(2);1+racine(2)[U]racine(7);infini[

c'est faux.

mais la ou je ne comprends pas c'est par exemple pour ]-infini ; -2[ ,
nous obtenons S1=]-infini;-racine(7)[U]racine(7);infini[ . Or les valeurs de x appartiennent que pour ]-infini;-racine(7)[ donc S1 est vrai que pour ]-infini;-racine(7)[ ?

oui.

Il y a quatre intervalles de définition, disons
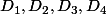
Il y a quatre ensembles de solution

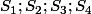
L'ensemble des solutions S est

[waterloo]

Très bien merci à vous !

[mathelot]

détaillons:

1er cas:



2eme cas:



3ème cas




4eme cas


x>3