Suite récurrente convergeant vers (√5-1)/2
13 messages
- Page 1 sur 1
Suite récurrente convergeant vers (√5-1)/2
Bonjour je bloque pour la question 4. Pourriez-vous m'aider svp ?
\textrm{ la suite d\'efinie par }u_0=0\textrm{ et }u_{n+1}=f(u_n)\textrm{ o\`u }f\textrm{ est la fonction de }\mathbb{R}\setminus\{-1\}\textrm{ dans }\mathbb{R}\\\\\textrm{d\'efinie par }f(x)=\dfrac{1}{x+1}.)
=x.\\\\\textrm{3. D\'emontrer que si le suite }(u_n)\textrm{ est convergente alors sa limite est \'egale \`a }\dfrac{\sqrt{5}-1}{2}.\\\\\textrm{4. On pose }l=\dfrac{\sqrt{5}-1}{2}.\\\\\textrm{(a) Montrer que }|u_{n+1}-l|<\dfrac{1}{2}|u_n-l|.\\\\\textrm{(b) En d\'eduire que pour tout }n\textrm{ dans }\mathbb{N}^*\textrm{, }|u_n-l|<\dfrac{1}{2^n}.\\\\\textrm{5. Montrer que la suite }(u_n)\textrm{ converge vers }\dfrac{\sqrt{5}-1}{2}.)
Modifié en dernier par checkmaths le 10 Jan 2019, 18:07, modifié 5 fois.
Re: Suite convergeant vers le nombre d'or
Modifié en dernier par checkmaths le 10 Jan 2019, 17:23, modifié 1 fois.
Re: Suite convergeant vers le nombre d'or
La résolution de f(x)=x ne donne pas ça
ou alors tu as mal écrit f(x)
vois avec
=\frac{1}{x}+1)
ou alors tu as mal écrit f(x)
vois avec
Re: Suite convergeant vers le nombre d'or
Bonjour
Même remarque @chan. Je doute que tu aies su faire la question 3!!!
Pas vu la réponse.
Donc c'est la question 2. qui pose pb.
Même remarque @chan. Je doute que tu aies su faire la question 3!!!
Pas vu la réponse.
Donc c'est la question 2. qui pose pb.
Re: Suite convergeant vers le nombre d'or
Modifié en dernier par checkmaths le 10 Jan 2019, 17:25, modifié 4 fois.
Re: Suite convergeant vers le nombre d'or
Rappel (de début de Lycée) :
^{\!2}\!-\!\big(\frac{1}{2}\big)^{\!2}\!\!-\!1=\big(x\!+\!\frac{1}{2}\big)^{\!2}\!-\frac{5}{4}=\big(x\!+\!\frac{1}{2}\!-\!\frac{\sqrt{5}}{2}\big)\big(x\!+\!\frac{1}{2}\!-\!\frac{\sqrt{5}}{2}\big))
est nul ssi un des termes du produit est nul, c'est à dire ssi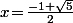 ou bien
ou bien 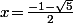
Et comme toujours, au lieu d'apprendre par cœur (et tel le no brain) des formules magiques pour au final les recracher de travers, est-ce que ça serait pas un tout petit peu plus intelligent de se rappeler la méthode (n'utilisant que des connaissances de collège) à employer pour résoudre ce type d'équation ?
est nul ssi un des termes du produit est nul, c'est à dire ssi
Et comme toujours, au lieu d'apprendre par cœur (et tel le no brain) des formules magiques pour au final les recracher de travers, est-ce que ça serait pas un tout petit peu plus intelligent de se rappeler la méthode (n'utilisant que des connaissances de collège) à employer pour résoudre ce type d'équation ?
Modifié en dernier par Ben314 le 10 Jan 2019, 17:13, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite convergeant vers le nombre d'or
ça colle toujours pas u(0)=0, alors u(1)=-1<0.
J'avais pas vu la correction de @chan, regardes un peu, s-t-p.
J'avais pas vu la correction de @chan, regardes un peu, s-t-p.
Re: Suite convergeant vers le nombre d'or
Il doit y avoir une erreur de signe dans le sujet... Je remets la définition de f de départ c'est-à-dire
=\dfrac{1}{x+1})
et je corrige la question 3, 4 et 5 :
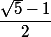
et je corrige la question 3, 4 et 5 :
Re: Suite récurrente convergeant vers (√5-1)/2
Ok ça va mieux.
Alors pour la 4 ème question tu peux par exemple appliquer le th des accroissement finis.
En effet) et f(l)=l.
et f(l)=l.
Alors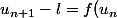-f(l)) ........
........
Alors pour la 4 ème question tu peux par exemple appliquer le th des accroissement finis.
En effet
Alors
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

 .
.