Bonjour,
J'ai des questions par rapport aux règles de calcul avec les racines nièmes.
si on peut écrire que:
n racines (a) = b
a = b^n
alors dans une équation ou inéquation comme par exemple:
racine ( 7x - 3) = 2x + 6
je peux écrire 7x - 3 = (2x + 6)^2 et ensuite la résoudre. Et ce cas mon ensemble de définition n'est pas D = [0 ; + infini [ ( vu que dans la racine ca doit etre toujours + ) mais D= R ?
et pour une inéquation ca ne modifie pas le sens de l'inégalité ?
Je vous remercie par avance de vos réponses
Cordialement.
Equation ou inequation avec racine
6 messages
- Page 1 sur 1
Re: equation ou inequation avec racine
D'abord tu as une condition sur le terme sous la racine, en effet 7x-3 doit être positif pour pouvoir écrire
racine(7x-3).
racine(7x-3).
Re: equation ou inequation avec racine
Bonjour,
ce n'est pas très clair.
Si x est positif, alors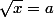 est équivalent à
est équivalent à  (par bijectivité de la fonciton racine), et
(par bijectivité de la fonciton racine), et  est équivalent à
est équivalent à  (par croissance de la fonction racine).
(par croissance de la fonction racine).
Si x n'est pas positif, alors est équivalent à
est équivalent à  .
.
Donc dans ton exemple, si tu dois résoudre

alors l'ensemble de définition est 7x-3 >=0 (ou x>= 3/7)
et cette équation est équivalente à résoudre
^2) sur
sur 
ce n'est pas très clair.
Si x est positif, alors
Si x n'est pas positif, alors
Donc dans ton exemple, si tu dois résoudre
alors l'ensemble de définition est 7x-3 >=0 (ou x>= 3/7)
et cette équation est équivalente à résoudre
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: equation ou inequation avec racine
Non ce n'etait pas du tout clair dans ma tête : ) . Merci à vous
Re: equation ou inequation avec racine
Là effectivement, ce n'est pas faux, mais si c'est pas faux, ça provient uniquement du fait que surSylviel a écrit:Si a est positif (1), alorsest équivalent à
(par bijectivité de la fonciton racine de [0,+oo[ sur [0,+oo[), et
est équivalent à
(2) (par croissance de la fonction racine).
(1) Et par contre dans le cas de l'équation, ça ne sert à rien de préciser "x positif" vu que c'est déjà écrit à la fois dans la relationet aussi dans la relation
.
(2) Par contre, effectivement, il faut le préciser dans le cas d'une inéquation
. . .
et cette équation est équivalente à résoudre
sur
Par contre si on avait à résoudre
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: equation ou inequation avec racine
Hum, oui pardon. Je me suis un peu embrouillé sur le coup. Ce que dis Ben est vrai,
 est équivalent à
est équivalent à  et
et 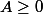
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
