Dérivée

[mehdi-128]

Bonjour,

Soit

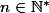
Soit tel que

Je veux montrer que la dérivée de f s'annule un nombre fini de fois. Donc ça donne :

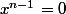
Mais j'ai oublié comment résoudre cette équation

[Landstockman]

Si pour a et b deux réels, ab=0, qu'est ce que tu peux dire de a ou de b ?

[pascal16]

n=1 -> l'équation est 1=0, pas de solution
n>1 -> 0 est la solution unique (de multiplicité n-1).

[mehdi-128]

Si pour a et b deux réels, ab=0, qu'est ce que tu peux dire de a ou de b ?

ou

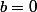
[mehdi-128]

n=1 -> l'équation est 1=0, pas de solution
n>1 -> 0 est la solution unique (de multiplicité n-1).

Ah d'accord merci. Vous avez utiliser la fonction racine n-ième ?

[Landstockman]

Si pour a et b deux réels, ab=0, qu'est ce que tu peux dire de a ou de b ?

ou

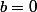
C'est ça !
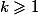
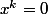
Du coup pour on en déduit (récurrence immédiate) que l'equation admet 0 comme unique solution.
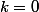
Le cas n'a pas de solution

[pascal16]

Ah d'accord merci. Vous avez utiliser la fonction racine n-ième ?

dans C, tu peux si tu veux
x= 0 * exp(2k*pi/(n-1)).....
le seule nombre complexe de norme nulle, c'est 0, le même que dans R.

[aviateur]

Bonjour,
Soit
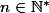
Soit tel que
Je veux montrer que la dérivée de f s'annule un nombre fini de fois. Donc ça donne :
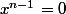
Mais j'ai oublié comment résoudre cette équation

Bonjour
C'est du surréalisme comme question?

[pascal16]

c'est X files en live, mais ça permet de mieux comprendre les phase de l'apprentissage.