Ker et injectivité

[Deura]

Bonjour tout le monde !
Pour finir 2018 en beauté ^^ on me demande de résoudre celà :

Soit E,F deux espaces vectoriels sur R et f : E -> F une application linéaire. Montrer que f est injective si et seulement si Ker(f) = {}.

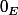
Je ne comprend pas comment faire.
Merci pour beaucoup votre aide

[mathelot]

bonjour,
supposons

Montrons que f est injective.
soient x et y dans E


f est linéaire...

[Deura]

Je ne comprends pas.
Pour montrer que f est injective, il faut que si f(x) = f(y) alors x=y non ?

[mathelot]

oui, sous l'hypothèse f(x)=f(y), il faut faire apparaitre x-y
car x=y équivaut à

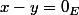
[Deura]

Donc ça donne :

Supposons que { }
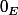
Montrons que f est injective
Soit x et y dans E


par linéarité
d'où

Je ne comprends pas où est-ce que l'on utilise l'hypothèse que { }

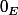
[Sa Majesté]

Donc ça donne :

Supposons que { }
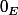
Montrons que f est injective
Soit x et y dans E tels que


par linéarité

Jusque là ça va (je rajouterais "tels que").

d'où

Là ça ne va pas.
Tu as
Que peux-tu dire de x-y ?

[Deura]

x-y représente le Ker de f donc ?

Mais pourquoi cela prouve que f est injective ?

[aviateur]

x-y représente le Ker de f donc ?

Mais pourquoi cela prouve que f est injective ?

Ta réponse montre que tu ne connais pas la définition de Ker f et cela explique aussi pourquoi tu ne comprends pas l'aide qu'on t'a fournie.
D'abord dire que "x-y représente le Ker f n'a pas de sens."
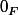
Ker f, je le rappelle, c'est l'ensemble des antécédents de par l'application f. Au demeurant c'est un sous ensemble de l'ensemble de départ E.
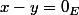
Alors signifie que x-y est un élément de Ker f mais comme alors donc x=y.

[Sylviel]

x-y est un élement de Ker(f).

[Deura]

D'accord. Je viens de comprendre.
Merci beaucoup pour votre aide et votre patience, et surtout bonne année