Question de base relation d'équivalence groupe quotient

[Poklo]

Bonjour,
J'ai une question de base sur la théorie des groupes, les groupes quotient :
Soit R la relation d'équivalence xRy : xH=yH
Je ne comprends pas l'équivalence :
xH=yH <=> (y^-1)*x appartient à H
Voici pourquoi je ne comprends pas la chose :
Je prends pour exemple :
Je me dis que -6+2 =-4 est dans 2Z
Donc 6*2Z=2*2Z ? Ce qui est bien entendu faux.

Je fais une faute absurde que je ne comprends pas
Merci de m'éclairer!
Bien à vous.

[Ben314]

Salut,
La "faute absurde", c'est de ne pas tenir compte de la loi de ton groupe. Dans la pratique, la loi d'un groupe, ça peut être un peu n'importe quoi, par exemple,parmi les liste de groupe "classique", il y a :


Sauf que dans ton cours, ben c'est bien précisé au début que la loi sera systématiquement notée multiplicativement pour énoncer les théorèmes (et donc qu'il faudra changer la notation dans le cas d'exercices où la loi n'est pas noté de la même façon).
Bref, là, visiblement, tu parle d'entier, c'est à dire d'élément de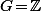 et sur cet ensemble, la loi standard (i.e. qui muni 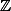d'une structure de groupe), ben c'est l'addition. Donc si tu prend par exemple le sous group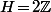e de (c'est à dire l'ensemble des multiples de 2 qui est clairement un sous groupe additif de 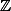) et l'élément 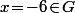, ben la classe de modulo qui dans le cours est noté 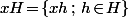(notation multiplicative) ben ici, c'est 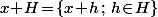(notation additive) c'est à dire qui est bien évidement égal à 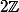ainsi qu'à .

De toute façon, des classes modulo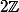 , il y en a évidement que deux, à savoir 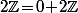lui même (=ensemble des nombres pairs) et (=ensemble des nombres impairs).

Et plus généralement, dans le contexte d'une loi (commutative) notée additivement, le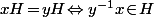 de ton cours, il devient 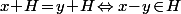. Par exemple, dans le cas de 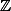ben tu retombe sur le résultat "de base" qui défini la notion de "congruences modulo ", à savoir que 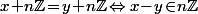et c'est cette fameuse égalité 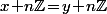que l'on note dans les petites classes ( congru à modulo ).

[Poklo]

Evidemment !..
J'avais bien considéré la loi additive sur le groupe (Z,+) dans mon exemple. Mais j'ai quand même fait l'erreur que vous avez décrite. Merci pour votre explication !