Période

[mehdi-128]

Bonjour,

Soit

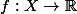
Le réel est une période de si :


Montrer que si est une période de alors est une période de .

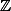
Je sais comment faire mais dois-je faire une récurrence sur où juste dire que ça marche par itération ?

[Landstockman]

Ça paraît un peu lourd une récurrence pour ça quand même...
C'est un sujet de quel niveau ?

[mehdi-128]

C'est un exemple dans mon livre de MPSI mais j'essaie de toute démontrer.

[Landstockman]

Et bien si tu le fais pour toi tu peux te contenter de considérer ça comme trivial, mais si tu veux tu peux toujours faire une récurrence^^

[mehdi-128]

J'ai fait de cette façon :

Comme alors

Comme alors

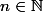
Soit par itération on obtient :

et

Enfin :

On fait la même chose pour

[Landstockman]

Tu n'as pas besoin de traiter le cas n=2 vu que tu as déjà le cas n=1

Mais sinon oui c'est évidemment juste (tu n'as pas besoin de rédiger ce genre de raisonnements, vu la facilité de la preuve on peut admettre directement le résultat)

[mehdi-128]

Ok merci mais ça me fait travailler la définition d'une période pour rien oublier dans les hypothèses.