Bonsoir,
Je me trouve coincé dans ces exercices. J'aimerais une aide.
https://ibb.co/4gBV86x
Olympiades
9 messages
- Page 1 sur 1
Re: Olympiades
Salut,
Le 1), on peut sûrement chercher des méthodes subtiles, mais même avec zéro réflexion, on y arrive avec que et exclusivement que du calcul bébète :
Ce que l'énoncé te demande de faire, c'est de déterminer les valeur de (dans
(dans  ) telles que le système
) telles que le système
^{\!3}\!+\!1\!+\!3\frac{x^2}{y}\!=\!x^3\end{matrix}\right.<br />\Leftrightarrow\ \left|\begin{matrix}y\!=\!\frac{x}{tx\!-\!1}\ \text{ avec }tx\!-\!1\!\not=\!0\hfill\cr (tx\!-\!1)^3\!+\!1\!+\!3x(tx\!-\!1)\!=\!x^3\frac{\null }{\null }\end{matrix}\right.)
possède au moins une solution\!\in\!\big({\mathbb R}^*\big)^{\!2}) , c'est à dire ssi il y a un
, c'est à dire ssi il y a un 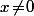 et tel que
et tel que 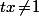 vérifiant
vérifiant
x^3\!-\!3t(t\!-\!1)x^2\!+\!3(t\!-\!1)x\!=\!0) soit
soit  (et
(et  quelconque) ou bien
quelconque) ou bien x^2\!-\!3tx\!+\!3\!=\!0)
de discriminant\!=\!-3(t\!+\!2)^2) qui conduit à une solution en
qui conduit à une solution en  uniquement lorsque
uniquement lorsque 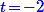 .
.
Le 1), on peut sûrement chercher des méthodes subtiles, mais même avec zéro réflexion, on y arrive avec que et exclusivement que du calcul bébète :
Ce que l'énoncé te demande de faire, c'est de déterminer les valeur de
possède au moins une solution
de discriminant
Modifié en dernier par Ben314 le 15 Déc 2018, 10:42, modifié 4 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Olympiades
Bonjour
Ok il y a un cas particulier avec 1/x+1/y=-2.
Voici comment j'ai fait avec des calculs simples.
On a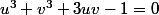
On pose s=u+v et p=uv donc
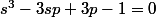
Ou encore
(1+s+s^2-3*p)=0)
Mais on a toujours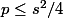
Donc^2)
Donc s=1 ou s=-2.
Si s=-2, p=s^2/4=1 dans ce cas effectivement x=y=-1 convient.
Mais u=1-v donne u^3+(1-u)^3+3 u (1-u)-1=0 tout de même.
Il y a donc une infinité de couple solutions qui donne u+v=1 i.e 1/x+1/y=1.
Ok il y a un cas particulier avec 1/x+1/y=-2.
Voici comment j'ai fait avec des calculs simples.
On a
On pose s=u+v et p=uv donc
Ou encore
Mais on a toujours
Donc
Donc s=1 ou s=-2.
Si s=-2, p=s^2/4=1 dans ce cas effectivement x=y=-1 convient.
Mais u=1-v donne u^3+(1-u)^3+3 u (1-u)-1=0 tout de même.
Il y a donc une infinité de couple solutions qui donne u+v=1 i.e 1/x+1/y=1.
Modifié en dernier par aviateur le 14 Déc 2018, 19:35, modifié 1 fois.
Re: Olympiades
Rebonjour
Pour l'exercice 2 en utilisant les similitudes on peut montrer que le rapport de l'aire du triangle
CBP par l'aire du triangle PCD est égal au rapport des longueur des cotés du parallélogramme ABCD. Ce qui implique que les hauteurs de ces deux triangles (hauteurs qui s'appuient sur les côtés du #) sont égales [CP) est donc bissectrices de l'angle BCD
Pour l'exercice 2 en utilisant les similitudes on peut montrer que le rapport de l'aire du triangle
CBP par l'aire du triangle PCD est égal au rapport des longueur des cotés du parallélogramme ABCD. Ce qui implique que les hauteurs de ces deux triangles (hauteurs qui s'appuient sur les côtés du #) sont égales [CP) est donc bissectrices de l'angle BCD
Re: Olympiades
Pour le 2), à froid, je vois pas de façon immédiate de méthode géométrique (alors qu'il y en a forcément une).
Mais avec de l'analytique, c'est plutôt simple :
On prend un repère) avec
avec 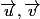 unitaires tels que dans ce repère on ait
unitaires tels que dans ce repère on ait ) et
et ) alors
alors ) ;
; ) ;
; ) et
et 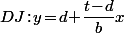 ce qui donne
ce qui donne ) ce qui montre que
ce qui montre que  est sur la première bissectrice du repère donc sur la bissectrice de l'angle (vu que les deux vecteur du repère ont même norme).
est sur la première bissectrice du repère donc sur la bissectrice de l'angle (vu que les deux vecteur du repère ont même norme).
Mais avec de l'analytique, c'est plutôt simple :
On prend un repère
Modifié en dernier par Ben314 le 15 Déc 2018, 13:33, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Olympiades
Exercice 1:
posons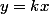 on arrive à
on arrive à =0)
Cette équation admet une racine réelle (merci Sagemath)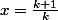
Tout les couples) ou
ou ) sont donc solutions.
sont donc solutions.
Les autres racines sont - 1) + I\sqrt(3) - 1}{k}) et
et  - 1) - I\sqrt(3) - 1}{k}) qui donnent -1 pour k=1, aux solutions ci-dessus il faut ajouter le couple (-1,-1)
qui donnent -1 pour k=1, aux solutions ci-dessus il faut ajouter le couple (-1,-1)
posons
Cette équation admet une racine réelle (merci Sagemath)
Tout les couples
Les autres racines sont
Re: Olympiades
salut
une variante pour le 1, un peu longue
on divise tout par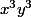 et on pose
et on pose 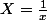 et
et 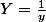
L'égalité initiale devient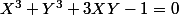
Il faut donc trouver toutes les valeurs possibles de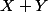 .
.
On factorise:
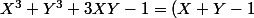(X^2+Y^2-XY+X+Y+1))
Le premier facteur donne comme possibilité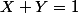
Pour le second facteur, on pose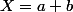 et
et 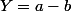
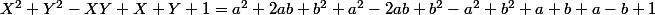
soit après simplification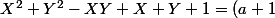^2+3b^2)
Le second facteur est nul seulement dans le cas: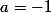 et
et 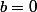 soit
soit 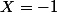 et
et 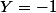
ce qui donne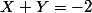
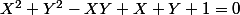 est l'équation d'une conique réduite au point (-1;-1)
est l'équation d'une conique réduite au point (-1;-1)
Exemples
Pour la solution=(-1,\frac{1}{2})) de l'équation initiale on a
de l'équation initiale on a 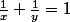
Pour la solution=(-1,-1)) on a
on a 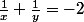
Remarques concernant geogebra (version Geogebra Classic 5.0.516.0-d):
Lorsqu'on entre l'équation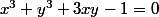 , il n'affiche que la droite
, il n'affiche que la droite 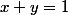 alors qu'il devrait mettre aussi le point (-1,-1)
alors qu'il devrait mettre aussi le point (-1,-1)
Lorsqu'on entre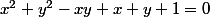 , il met bien ce point
, il met bien ce point

une variante pour le 1, un peu longue
on divise tout par
L'égalité initiale devient
Il faut donc trouver toutes les valeurs possibles de
On factorise:
Le premier facteur donne comme possibilité
Pour le second facteur, on pose
soit après simplification
Le second facteur est nul seulement dans le cas:
ce qui donne
Exemples
Pour la solution
Pour la solution
Remarques concernant geogebra (version Geogebra Classic 5.0.516.0-d):
Lorsqu'on entre l'équation
Lorsqu'on entre

9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
