Svp aidez moi à résoudre cette équation
|6-x|+|x+1|=2-|x|
Valeur absolue
5 messages
- Page 1 sur 1
Re: Valeur absolue
bonsoir,
les quantités à l'intérieur des valeurs absolues changent de signe en s'annulant pour les valeurs de x!
-1;0;6
on distingue alors quatre cas:
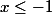
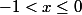
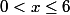
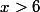
pour chaque cas, ôter les valeurs absolues.
|x| = x si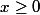
|x|=-x si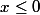
les quantités à l'intérieur des valeurs absolues changent de signe en s'annulant pour les valeurs de x!
-1;0;6
on distingue alors quatre cas:
pour chaque cas, ôter les valeurs absolues.
|x| = x si
|x|=-x si
Re: Valeur absolue
Bonjour;
En suivant les conseils de Mathelot , tu dois arriver à construire le tableau suivant :
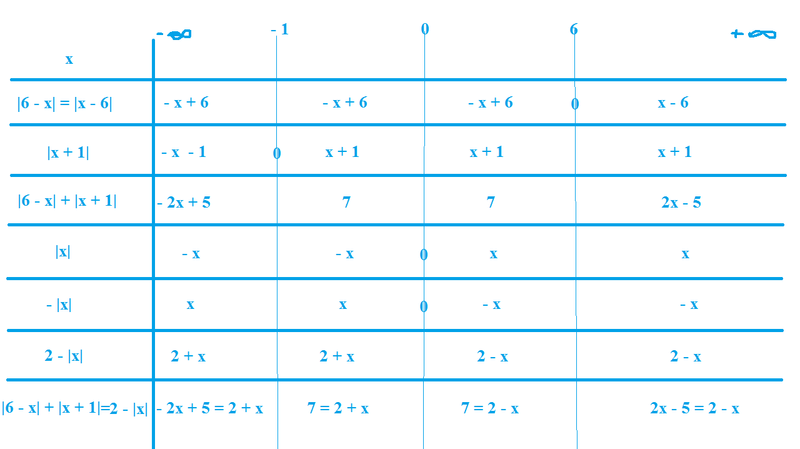
Tu dois maintenant résoudre les équations obtenues et conclure .
La figure ci-dessous t'aideras à vérifier les résultats obtenus .
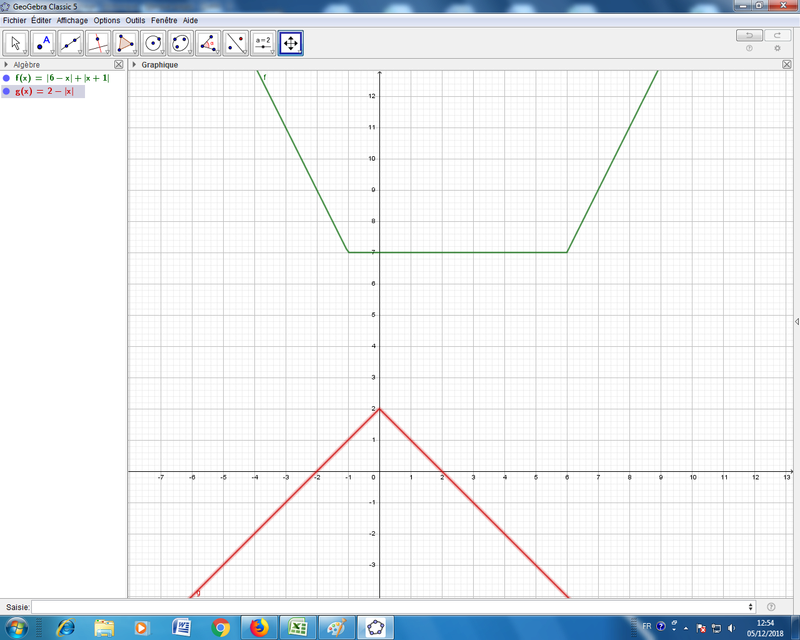
En suivant les conseils de Mathelot , tu dois arriver à construire le tableau suivant :

Tu dois maintenant résoudre les équations obtenues et conclure .
La figure ci-dessous t'aideras à vérifier les résultats obtenus .

Re: Valeur absolue
Salut,
|6-x|+|x+1| = 2-|x|
Le membre de gauche est > 0 et donc |x| < 2
--> x dans ]-2 ; 2[ et donc, on a : 4 < |6-x| < 8 (1)
|x+1| + |x| = 2 - |6-x| et avec (1) -->
|x+1| + |x| < 0 ce qui est impossible ---> Pas de solution.

|6-x|+|x+1| = 2-|x|
Le membre de gauche est > 0 et donc |x| < 2
--> x dans ]-2 ; 2[ et donc, on a : 4 < |6-x| < 8 (1)
|x+1| + |x| = 2 - |6-x| et avec (1) -->
|x+1| + |x| < 0 ce qui est impossible ---> Pas de solution.
Re: Valeur absolue
Bonjour à toutes et à tous, des explications vraiment claires. Grand bravo les amis et merci à vous d'être là pour nous aider.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
