Ordre et calcul dans R
14 messages
- Page 1 sur 1
Ordre et calcul dans R
Bonsoir je ne m'y retrouve vraiment pas en démonstration. Alors j'aimerai beaucoup qu'on m'aide
Démontrer les inégalités suivantes
A)x/y + y/x 》2
B) si x <y alors x <\sqrt {xy}<y
C) 1/x+y <1/x + 1/y
X, Y, X positifs
1) je compare x/y et x+z/y+z
Démontrer les inégalités suivantes
A)x/y + y/x 》2
B) si x <y alors x <\sqrt {xy}<y
C) 1/x+y <1/x + 1/y
X, Y, X positifs
1) je compare x/y et x+z/y+z
Re: Ordre et calcul dans R
Salut, (les x,y sont strictement positif je suppose ?)
1) Je te propose plutôt de montrer que :
 (tu en déduiras le résultat que tu veux en prenant un a bien choisis)
(tu en déduiras le résultat que tu veux en prenant un a bien choisis)
Pour montrer cela je te conseille de regarder :^2)
2) c'est plutôt simple tu as juste à utiliser la stricte croissance de la fonction racine sur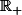
3) Surement une faute ??? Ce que tu as écris est équivalent à ce qui est évidemment faux.
ce qui est évidemment faux.
1) Je te propose plutôt de montrer que :
Pour montrer cela je te conseille de regarder :
2) c'est plutôt simple tu as juste à utiliser la stricte croissance de la fonction racine sur
3) Surement une faute ??? Ce que tu as écris est équivalent à
Re: Ordre et calcul dans R
A) Montre que x/y + y/x <2 aboutit à une contradiction pour monter x/y + y/x <= 2.
B) Comme dit infernaleur
C) Bah non tu te trompes infernaleur refais tes calculs... Montre par l'absurde comme dans A).
B) Comme dit infernaleur
C) Bah non tu te trompes infernaleur refais tes calculs... Montre par l'absurde comme dans A).
Re: Ordre et calcul dans R
Ahaha j'aimerais bien pouvoir m'aider de vos techniques mais malheureusement les techniques utilisées par vous (fonctions, R+...) me sont inconnues. On les a pas encore fait à l'école. Ces démonstrations sont du niveau d'une simple classe de seconde S. Merci quand même
Re: Ordre et calcul dans R
C'est une meilleure idée alors si vous précisez votre classe là prochaine fois, comme ça, vous aurez l'explication qui vous convient. N'est-ce pas?
Re: Ordre et calcul dans R
Bonjour;
\in\mathbb R^{*+2} : \dfrac{x}{y} + \dfrac{y}{x}\ge 2\Leftrightarrow\dfrac{x^2+y^2}{xy}\ge2\Leftrightarrow\dfrac{x^2+y^2}{xy}-2\ge0)
^2}{xy}\ge0) : cette proposition est vraie , donc la proposition du début est vraie .
: cette proposition est vraie , donc la proposition du début est vraie .
Re: Ordre et calcul dans R
Mais pour la c , il doit manquer une parenthèse
si et
et  sont des réel positifs , on peut dèja montrer ceci
sont des réel positifs , on peut dèja montrer ceci  puis minorer le membre de gauche pour aboutir au résultat voulu non?
puis minorer le membre de gauche pour aboutir au résultat voulu non?
si
Re: Ordre et calcul dans R
Bonsoir,
Vous avez utilisé la croissance de la fonction racine carrée pour répondre à cette question.Pour la question c, je suspecte une parenthèse manquante au dénominateur ,d'ou l'objet de mon interrogation.En corrigeant , on y verrait une belle Qu'en pensez vous?
Qu'en pensez vous?
Sinon pour la b
j 'ai fait autrement
\in\mathbb R^2^+}) :
:
 }^{ 2 }\ge 0\quad \Leftrightarrow \quad x+y\ge 2\sqrt { xy } \Leftrightarrow \dfrac { x+y }{ 2 } \ge \sqrt { xy } \\)
c'est une (AM-GM)
si

donc ,
\in\mathbb R^2^+}) tel que
tel que 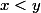 on a:
on a: 
Vous avez utilisé la croissance de la fonction racine carrée pour répondre à cette question.Pour la question c, je suspecte une parenthèse manquante au dénominateur ,d'ou l'objet de mon interrogation.En corrigeant , on y verrait une belle
Sinon pour la b
j 'ai fait autrement
c'est une (AM-GM)
si
donc ,
Re: Ordre et calcul dans R
Pour la a , j 'ai aussi fait autrement
Je me suis dit comme tous les réels sont positifs autant prendre les carrées de chaque membre.:
\in\mathbb R^2^*^+}) :
:  }^{ 2 }\ge 4\quad \Leftrightarrow \dfrac { { x }^{ 2 } }{ { y }^{ 2 } } +\dfrac { { y }^{ 2 } }{ { x }^{ 2 } } \ge 2\Leftrightarrow { x }^{ 4 }+{ y }^{ 4 }\ge 2{ \left( xy \right) }^{ 2 }\Leftrightarrow { \left( { x }^{ 2 }-{ y }^{ 2 } \right) }^{ 2 }\ge 0)
Un carré est tjrs positifs
Je me suis dit comme tous les réels sont positifs autant prendre les carrées de chaque membre.:
Un carré est tjrs positifs
Re: Ordre et calcul dans R
descampsh a écrit:C'est une meilleure idée alors si vous précisez votre classe là prochaine fois, comme ça, vous aurez l'explication qui vous convient. N'est-ce pas?
Vous avez raison. J'aurais du préciser
Re: Ordre et calcul dans R
[quote="fastandmaths"]
Merci cette demonstration de la a m'a aidée. Par contre pour la B, votre methode était assez compliquée. N'en aurez vous pas de plus simple ?(pour que je puisse comprendre ?)
Merci cette demonstration de la a m'a aidée. Par contre pour la B, votre methode était assez compliquée. N'en aurez vous pas de plus simple ?(pour que je puisse comprendre ?)
Re: Ordre et calcul dans R
Salut ,
"aymanemaysae" a tout dit concernant la b , il utilise le fait que la fonction racine est strictement croissante sur R^+, je ne pense pas que tu puisses trouver plus simple que sa démonstration.
"aymanemaysae" a tout dit concernant la b , il utilise le fait que la fonction racine est strictement croissante sur R^+, je ne pense pas que tu puisses trouver plus simple que sa démonstration.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
