Adhérence des matrices diagonalsables dans R

[protozik10012]

Bonjour tout le monde,j'ai un petit souci à propos d'un exercice et je demande votre aide..


Montrer que si λ appartient à R est racine du polynome Q=X^n + anX^n-1 + .....+ a1X + a0 ,alors |λ|<=nM

avec M majorant de 1,|a0|,......,|a(n-1)|

merci pour votre aide

[aviateur]

Bonjour
D'abord une remarque: je ne vois pas pourquoi on se limite à l'exercice reste valable si les coeff sont dans C ainsi que la racine.
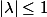
Si l'inégalité est vérifiée. On suppose maintenant que
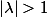
On a

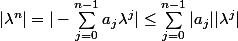
dc

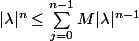
d'où le résultat.
Autre remarque la majoration est très (très) grossière on peut faire beaucoup mieux.
Penser à la matrice de Frobienus et le théorème de Gerschgorin lemme d'Hadamard.

[protozik10012]

Merci beaucoup aviateur j'avais pensé à cette méthode mais j'ai pas fait attention à la majoration

Pour C c'est général ,je suis d'accord.