Salut à tous, Besoin d'aide
en utilisant l'algorithme d'euclide determiner les entiers naturels a et b sachant qu'on a eu dans la division euclidienne de a par b les quotients suivants; 1,2,1,1,2 et que pgcd(a,b)=5
ARITHMETIQUE
12 messages
- Page 1 sur 1
Re: ARITHMETIQUE
Salut,
Je comprend que dalle à ce que ça veut dire : quand on divise a par b, des quotients, on en a un et un seul et je vois franchement ce que ça peut vouloir dire que LES quotients sont égaux à . . .
Je comprend que dalle à ce que ça veut dire : quand on divise a par b, des quotients, on en a un et un seul et je vois franchement ce que ça peut vouloir dire que LES quotients sont égaux à . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: ARITHMETIQUE
ce sont les quotients (en chiffre) à chaque étape de l'algorithme de division euclidienne
Re: ARITHMETIQUE
Ben314 a écrit:Salut,
Je comprend que dalle à ce que ça veut dire : quand on divise a par b, des quotients, on en a un et un seul et je vois franchement ce que ça peut vouloir dire que LES quotients sont égaux à . . .
Ben314 désolé pour le manque de précision! je voulais dire les quotients à chaque étape de la division euclidienne lorsqu'on fait l'algorithme d'Euclide
Re: ARITHMETIQUE
Si c'est effectivement les quotient qu'on obtient à chaque itération lorsque l'on fait la division en base 10, je trouve ça bizarre comme formulation : ça aurait été plus simple de simplement dire que le quotient s'écrit 12112... en base 10.mathelot a écrit:ce sont les quotients (en chiffre) à chaque étape de l'algorithme de division euclidienne
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: ARITHMETIQUE
Si ces fameux 1,2,1,1,2 c'est les quotients successifs dans l'algo. d'Euclide et que ce dernier s’arrête après le dernier 2 en donnant un pgcd=5, ben c'est complètement culcul comme exercice : il suffit de savoir ce que c'est que ce fameux "algorithme d'Euclide", de l'écrire en "remontant" les étapes.
Bref, ça consiste à écrire quoi cet algo. d'Euclide ?
Bref, ça consiste à écrire quoi cet algo. d'Euclide ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: ARITHMETIQUE
salut
unefaçon:
Ecris les égalités correspondant aux 5 divisions euclidiennes
tu peux appeler les restes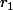 ,
, 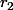 ,
, 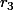 ...
...
tu dois trouver a=90
unefaçon:
Ecris les égalités correspondant aux 5 divisions euclidiennes
tu peux appeler les restes
tu dois trouver a=90
Re: ARITHMETIQUE
l'algo d'Euclide permet de retrouver ce pgcd=9 en fait ce pgcd est le dernier reste non nul des divisions succesives
Re: ARITHMETIQUE
chan79 a écrit:salut
unefaçon:
Ecris les égalités correspondant aux 5 divisions euclidiennes
tu peux appeler les restes,
,
...
tu dois trouver a=90
Quand jecris les divisions succesives et j'essaie de remonter j'arrive à la fin à 13a-18b=9 c'est bien sa?
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
