Démonstration limite P(X)exp(x)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Deura
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2018, 16:26
-
 par Deura » 25 Nov 2018, 16:24
par Deura » 25 Nov 2018, 16:24
Oyez braves gens.
Par ce beau dimanche, me voilà tombé sur un os.
Soit P une fonction polynomiale. Démontrer que
 e^{-x} = 0)
En soit, ça parait évident. La fonction exponentielle est la "plus forte". Mais comment le démontrer ?
Merci pour vos réponses

et bonne journée !
-
mathelot
 par mathelot » 25 Nov 2018, 16:51
par mathelot » 25 Nov 2018, 16:51
bonjour
pour tout x réel
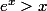
soit n fixé; x>0

en élevant à la puissance n+1 (croissante sur
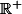
)
^{n+1}})
^{n+1}})
d'où pour n fixé

en passant à l'inverse:

Si

est un polynôme de degré n et de coefficient dominant

non nul:
 e^{-x}=\lim_{x \rightarrow +\infty} \, a_n x^n (1+o(1)) e^{-x}=0)
o(1) est (désigne) une fonction de limite nulle
-
Deura
- Membre Naturel
- Messages: 30
- Enregistré le: 29 Oct 2018, 16:26
-
 par Deura » 25 Nov 2018, 17:05
par Deura » 25 Nov 2018, 17:05
Whouaa
Merci beaucoup mathelot pour ta réponse complète et rapide

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
 et bonne journée !
et bonne journée ! et bonne journée !
et bonne journée !