
Problèmes (factorisation et racines carrées)
7 messages
- Page 1 sur 1
 Problèmes (factorisation et racines carrées)
Problèmes (factorisation et racines carrées)
Bonjour, j'aimerais savoir comment résoudre ces deux problèmes.


Re: Problèmes (factorisation et racines carrées)
pour la 1B)) on a:
Les racines du polynôme
des racines cinquièmes de l'unité.
or
Re: Problèmes (factorisation et racines carrées)
mathelot a écrit:
on utilise les polynômes
avec
Modifié en dernier par mathelot le 25 Nov 2018, 21:31, modifié 2 fois.
Re: Problèmes (factorisation et racines carrées)
Exercice 1A)
factoriser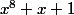
soit j le complexe tel que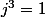 et
et 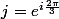

=j^2+j+1 =0)
Par conjugaison
=j^{16}+j^2+1=j+j^2+1=0)
donc A est divisible par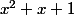
en faisant la division euclidienne des polynômes:
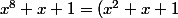(x^6-x^5+x^3-x^2+1))
factoriser
soit j le complexe tel que
Par conjugaison
donc A est divisible par
en faisant la division euclidienne des polynômes:
Re: Problèmes (factorisation et racines carrées)
pour le 1B)
soit et
et  les racines troisième de l'unité:
les racines troisième de l'unité:
il vient
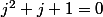 et
et 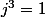
montrons que j est racine de
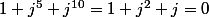 car
car 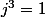
montrons que est racine de
est racine de 
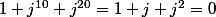 car
car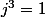
donc est divisible par
est divisible par(X-j^2)=X^2+X+1)
soit
il vient
montrons que j est racine de
montrons que
donc
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
