OLYMPIADES

[mouadbouski]

Bonsoir, je viens de passer un examen d'olympiades de mathématiques composé de trois exercices et j'aimerais des démonstrations précises pour chaque exercice pour m'aider à comprendre bien l'énoncé et les méthodes de réponse. J'ai trouvé que c'est difficile quand même de faire ces exercices en 2 heures.
J'ai réécris les problèmes sur WORD ensuite j'ai fais une capture d'écran que vous allez la trouver
sur ce site :

MERCI

[FLBP]

Salut,
je commence par le 2 car il est assez simple:
- Soit la projection du point sur .
- Soit la hauteur
- Soit d la distance
La somme des carrés depuis le point peut s'exprimer ainsi:
// c'est l'hypothenus du triangle , rectangle en

Si on développe:


On applique la règle de la hauteur:


















Je regarde la suite ...

[Ben314]

Salut,

Le 1), il est pas bien méchant. Si on note (1) ; (2) et (3) les 3 équations, alors on a :

- Si alors (1) donne puis (3) donne donc et (et (2) est bien vérifiée)
- Si alors donne qui, avec (1), donne et puis (3) donne donc (et (2) est bien vérifiée)
Il y a donc deux solutions dans R : ( 1 , -1 , 1 ) et ( -1 , -1 , -1 )

Et le 3), c'est pas bien méchant non plus :
L'énoncé te dit qu'il existe un entier naturel non nul tel que .
.

Il y a donc deux solutions : a=b=1 ainsi que a=1 ; b=3.

[mouadbouski]

Ben314
Il y a aussi (x,y,z)=(0,-1,0) que j'ai vu dans la calculatrice et quand j'ai vérifié, la réponse était vrai mais je ne sais pas comment la montrer.

[Ben314]

Ben ça serait pas con de commencer par apprendre à compter : si ; et alors ça vaut 0 - 1 + 0 = -1 et pas 1 donc la deuxième équation n'est pas vérifiée.

[FLBP]

"que j'ai vu dans la calculatrice"

Tu vois aussi le futur là dedans ?

[Ben314]

Sinon, j'avais pas regardé le 2 vu que FLBP l'avais fait, mais il déconne :
Dans l'énoncé, rien ne dit que les sont distincts ni que ni même qu'il y a une unique disposition des (l'énoncé dit bien que les sont "DES points tels que" et pas "LES points tels que").
Donc une situation envisageable, c'est (entre autre)

milieu de

Sauf que dans ce cas, l'égalité demandée n'est pas vérifiée.

Je sais pas à quel niveau c'est le bidule, mais si c'est un tant soit peu élevé, l'épreuve va être annulée vu que ça m'étonnerais qu'aucun participant n'ai repéré l'erreur.

Et sinon, c'est effectivement assez désespérant de voir le nombre d'élèves pour lequel la calculatrice fait office de cerveau....

[FLBP]

Salut Ben,
Je crois bien que dans le cas que tu as cité l'égalité est vérifiée :
- soit la médiane en du triangle rectangle en .

[FLBP]

Ah j'avais mal lu, il n'y a pas autant de points allant à B que ceux allant à A alors non, tu avais raison

[Ben314]

Tient, les énoncée ont changés....

Pour l'exo 1), les 3 inéquations impliquent que :

c'est à dire où
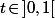
Or, pour tout on a :

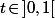
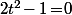
donc pour tout on a avec égalité ssi c'est à dire .
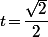
L'inégalité n'est donc vérifiée que pour et il est clair que dans ce cas là, les trois inégalités de départ sont bien vérifiées.

L'exercice 2) il est totalement couillon : si on note la symétrie orthogonale par rapport à (AK) alors :
- Vu que (AK), est la bissectrice de l'angle (BAC), envoie la droite (AB) sur (AC).
- Vu que le triangle ADK est rectangle en D, son cercle circonscrit c'est celui de diamètre [AK] donc la symétrie laisse le cercle globalement invariant.
Et on en déduit évidement que s(E)=F et donc que AE=AF.