Espaces vectoriels
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
manianga
- Membre Naturel
- Messages: 55
- Enregistré le: 07 Jan 2006, 19:22
-
 par manianga » 11 Nov 2006, 14:09
par manianga » 11 Nov 2006, 14:09
bonjour j'ai un souci avec cet exercice pourriez vous m'aider svp?
vérifier que l'ensemble S des (x,y,z) de R^3 tels que x^2+2y^2+2z^2+2xy+2zx=0 est un sous espace vectoriel de R^3.
je ne comprend pas comment on peut le demontrer
merci d'avance pur votre aide
-
hqckers
- Membre Naturel
- Messages: 73
- Enregistré le: 10 Nov 2006, 19:39
-
 par hqckers » 11 Nov 2006, 14:21
par hqckers » 11 Nov 2006, 14:21
je pense que déjà il faut ke tu connaisses les conditions nécessaires pour que cette ensemble soit une sous-espace vectoriel de R^3 et après tu les démontre
stabilité pour la loi + pour la LCE antitruc et que ton sous esemble soit une partie non vide de R^3
-
Vir
- Membre Naturel
- Messages: 23
- Enregistré le: 03 Juil 2006, 00:06
-
 par Vir » 11 Nov 2006, 14:24
par Vir » 11 Nov 2006, 14:24
Y a trois choses a montrer :
S non vide
Pour tout u,v de S, u+v appartient toujours à S
Et pour t de R, u*t appartient toujours à S
-
Easyblue
- Membre Relatif
- Messages: 344
- Enregistré le: 07 Nov 2006, 15:39
-
 par Easyblue » 11 Nov 2006, 14:30
par Easyblue » 11 Nov 2006, 14:30
si je me souviens bien de la définition d'un sous-espace vectoriel, tu dois montrer que S est non vide et que :




,

x,y

S alors

*x + y

S
-
hqckers
- Membre Naturel
- Messages: 73
- Enregistré le: 10 Nov 2006, 19:39
-
 par hqckers » 11 Nov 2006, 14:32
par hqckers » 11 Nov 2006, 14:32
euh il ne me semble pas que ce soit * mais plutôt antitruc ( mm signe de orthogonal ) car c la multiplication par un scalaire et non un élément de R^3
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 11 Nov 2006, 14:42
par abcd22 » 11 Nov 2006, 14:42
La multiplication par un scalaire se note « . » en général, et les trucs et antitrucs ça sert seulement quand on commence à voir les lois en sup/L1 (pour des lois internes plutôt), après on note plutôt +, x, ., * , rien... Pour les espaces vectoriels sur R c'est souvent (E,+,.), et on n'écrit pas le « . » quand on fait une multiplication par un scalaire en pratique.
-
manianga
- Membre Naturel
- Messages: 55
- Enregistré le: 07 Jan 2006, 19:22
-
 par manianga » 11 Nov 2006, 15:10
par manianga » 11 Nov 2006, 15:10
:triste: euh... désolé mais je n'arrive pas a vous comprendre je sais juste qu'il faut faire 3 demo la premiere avec 0 apres une addition puis une multiplication mais mon probleme c'est que je n'arrive pas faire ces 3 demo
-
Easyblue
- Membre Relatif
- Messages: 344
- Enregistré le: 07 Nov 2006, 15:39
-
 par Easyblue » 11 Nov 2006, 15:22
par Easyblue » 11 Nov 2006, 15:22
A mon avis, il faut que tu montre que (0,0,0) est solution.
Puis que si (x1,y1,z1) est solution et (x2,y2,z2) est solution alors (x1+x2,y1+y2,z1+z2) est solution.
Puis que si (x,y,z) est solution et si

appartient à

alors (

x,

y,

z) est solution.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Nov 2006, 15:48
par yos » 11 Nov 2006, 15:48
manianga a écrit:vérifier que l'ensemble S des (x,y,z) de R^3 tels que x^2+2y^2+2z^2+2xy+2zx=0 est un sous espace vectoriel de R^3.
J'ai pas envie de faire des calculs mais je verrais plutôt un ellipsoïde ou un truc de ce genre. Un sev, ça me surprendrait.
-
manianga
- Membre Naturel
- Messages: 55
- Enregistré le: 07 Jan 2006, 19:22
-
 par manianga » 11 Nov 2006, 15:58
par manianga » 11 Nov 2006, 15:58
je ne sais pas ce que c'est qu'un ellipsoide :help:
et comme on a jamais vu ca en cours je ne pense pas que ce soit ca que je doive démontrer.

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 11 Nov 2006, 16:41
par nuage » 11 Nov 2006, 16:41
Salut,
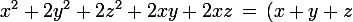^2+(y-z)^2)
.
Dans
R la somme de deux carrés est nulle ssi ils sont tous les deux nuls.
Aprés c'est plus facile.
A+
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 11 Nov 2006, 18:14
par yos » 11 Nov 2006, 18:14
OK c'est donc une droite. J'aurai dû faire les calculs! C'est malin comme exo.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
