Suites réelle

[Quanto]

Un=(1!+2!+3!+....n!)/n!
comment je fais pour montrer que cette suite est convergente? et comment on calcule sa limite ?

[Ben314]

Salut,
Montre que, pour tout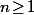 on a 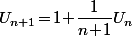puis que .

[Quanto]

je peux montrer Un+1 par contre l’autre inégalité sa paraît compliqué

[mehdi-128]

je peux montrer Un+1 par contre l’autre inégalité sa paraît compliqué

Par récurrence c'est simple.

[capitaine nuggets]

Re-Salut !

1. En majorant les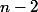 premiers termes de la somme , montre que :



2. Justifie que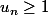 , quel que soit .

3. Déduis-en que :



4. Conclure alors en utilisant le théorème des gendarmes.

[fastandmaths]

Bonjour,

J'ai repris le sujet car le posteur n'a plus donner suite.

J'ai essayé de retrouver vos résultats en détaillant d 'avantage,est ce de cette manière que vous avez procédé pour borner la suite .Est il possible d 'étudier directement la monotonie de cette suite , puis montrer simplement qu'elle est majorée par 1?, car c 'était ma première intuition.

soit


on a :

donc,


ainsi


De la même manière on déduit que la suite est minorée par :

D'après le théoréme des gendarmes :

Merci

[fastandmaths]

Lire minoré par 1/(n)(n-1)(n-3)! +1/n. +1 j ai pris la mauvaise ligne