Les suites arithmético-géométriques niveau Terminale S

[walida33]

Bonsoir à tous,
Voici le sujet de l'exercice:

On dit qu'une suite (Un) De premier terme u0 Non nul est arithmetico-géométrique Si elle est définie pour Tout n appartenant à N par Un*1= aUn+b avec a appartenant à R\{0;1} et b appartenant à R*.

1) Expliquer pourquoi on impose a =/= 0, a=/= 1 et b=/=0
Dans le premier cas, Un devient constante, dans le second, Un devient arithmétique et dans le dernier cas elle devient géométrique.

2) Montrer que la suite (Un) est constante Si et seulement Si u0= b/(1-a).
J'ai réussi à repondre.

Dans la suite, on considère u0 =/= b/(1-a) et on admet qu'alors, aucun terme de (Un) n'est égal à b/(1-a).

3) justifier que la suite (Vn) définie par Vn= Un- (b/(1-a)) pour Tout n appartenant à N est géométrique.

Alors j'ai un problème avec cette question. Je n'arrive pas du tout à la résoudre.
Je sais que b/(1-a) représente la valeur que doit prendre u0 pour que (Un) soit constante et qu'une suite constante est définie par Un+1=b.

Pourriez-vous me donner quelques pistes?
Merci d'avance.

[Ben314]

Salut,
Perso., la façon dont je rédige ce type de truc, c'est pas vraiment celle qu'on trouve le plus fréquemment au Lycée (et que je trouve pas mal con...).
- Tu as une formule qui donne, pour tout entier n en fonction de
- Cette formule, tu peut facilement "s'inverser" pour avoir en fonction de
- Et bien sûr, tu as aussi la formule de départ qui donne en fonction de .

Maintenant, partant de ,
- En utilisant (1) tu peut l'écrire en fonction de .
- Puis en utilisant (3) tu peut l'écrire en fonction de .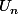
- Puis en utilisant (2) tu peut l'écrire en fonction de .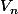

Et la "logique" qu'il y a derrière est complètement concon : c'est comme si tu trouvait sur le net une formule de je sais pas quoi qui exprime la longueur d'un "résultat" en fonction de celle d'un "truc de départ", mais que la formule donne tout en pouces alors que toi tu la veut en centimètres.
Ben il faut faire :
- Centimètres -> Pouces
- Pouces -> Pouces (avec la formule trouvée sur le net)
- Pouces -> Centimètres

[walida33]

D'accord merci beaucoup pour ta réponse du coup j'ai trouvé Vn+1 = aVn qui est bien une suite géométrique