Aaide pour developper
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 08:28
par Laur » 11 Nov 2006, 08:28
Bonjour dans mon exercice de mathematiques je dois:::::
a°) developper (a²-ab+b²)(a+b)
b°) utiliser l'identite remarquable obtenue en a pour factoriser :::
8a^3 +27b^3
puis
216x^3+125y^3
LE PROBLEME C'EST QU'A LA QUESTION a JE TROUVE a^3+b^3 ET CE N'EST PAS UNE IDENTITE REMARQUABLE COMMENT DOIS-JE PROCEDER ?????????
MERCI
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 11 Nov 2006, 08:43
par fonfon » 11 Nov 2006, 08:43
Salut,
indication
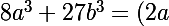^3+(3b)^3)
-
BancH
- Membre Irrationnel
- Messages: 1317
- Enregistré le: 17 Mar 2006, 21:50
-
 par BancH » 11 Nov 2006, 08:43
par BancH » 11 Nov 2006, 08:43
Ce que tu as trouvé c'est:
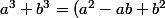(a+b))
Donc
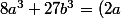^3+(3b)^3=...)
-
Emil34730
- Membre Naturel
- Messages: 18
- Enregistré le: 09 Nov 2006, 18:26
-
 par Emil34730 » 11 Nov 2006, 09:17
par Emil34730 » 11 Nov 2006, 09:17
Allez, je suis généreux, pour la seconde tu remplace les a et b par x et y et ca fait:
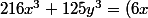^3 + (5x)^3)
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 09:45
par Laur » 11 Nov 2006, 09:45
je vous remercie tous je vais essaier merci de votre aide
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 10:25
par Laur » 11 Nov 2006, 10:25
donc si j'ai bien compris pour factoriser ( a²-ab+b²)(a+b) en identite remarquable::::
je vais obtenir:::
a^3+ab²-ab²-ab²+ab²+b^3
tous les ab² s'eliminent
j'obtiens a^3+b^3 ?????? (mais le probleme c'est que ce n'est pas une identite remarquable?????je ne comprends pas ...
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 11 Nov 2006, 10:40
par fonfon » 11 Nov 2006, 10:40
Laur a écrit:donc si j'ai bien compris pour factoriser ( a²-ab+b²)(a+b) en identite remarquable::::
je vais obtenir:::
a^3+ab²-ab²-ab²+ab²+b^3
tous les ab² s'eliminent
j'obtiens a^3+b^3 ?????? (mais le probleme c'est que ce n'est pas une identite remarquable?????je ne comprends pas ...
oui c'est bien a^3+b^3=(a²-ab+b²)(a+b)
or on te donne
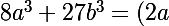^3+(3b)^3)
si tu appelles
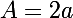
et

on a
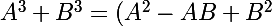(A+B))
donc
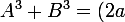^3+(3b)^3=....)
Ps;banch c'est (a²-ab+b²)(a+b) et non (a²
-2 ab+b²)(a+b)
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 11:06
par Laur » 11 Nov 2006, 11:06
merci fonfon je devrais y arriver merci a tous
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 11:35
par Laur » 11 Nov 2006, 11:35
oups................................
a^3+b^3
8a^3+27b^3
(2a)^3+(3b)^3
a=2a et b=3b
( (2a)²-2a fois 3b+(3b)² ) (2a+3b)
( 4a²-6ab+9b² ) (2a+3b )
8a^3+12ab²-12ab²-18ab²+18ab²+27b^3
8a^3+27b^3
(2a)^3+(2b)^3
mais c'est le depart ce n'est pas une factorisation aie aie aie....
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 11 Nov 2006, 11:38
par fonfon » 11 Nov 2006, 11:38
Re, pourquoi que une fois que tu as remplacer et tu redeveloppes la forme factorisé de a^3+b^3=(a²-ab+b²)(a+b) c'est tout
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 13:31
par Laur » 11 Nov 2006, 13:31
ok merci fonfon donc la forme factorisee c'est ::::
(4a²-6ab+9b²)(2a+3b)? la c'est la forme factorisee????ou je factorise encore les a ?
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 11 Nov 2006, 13:41
par Elsa_toup » 11 Nov 2006, 13:41
Oui c'est cela, mais tu peux factoriser la première expression...
Si tu transformes 4a² en (2a)² et 9b² en (3b)², tu devrais voir apparaître une identité reconnaissable....
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 14:04
par Laur » 11 Nov 2006, 14:04
bonjour Elsa toup vous voulez dire que ( 4a²-6ab+9b²)(2a+3b) est encore factorisable????
mais j'obtiens::
((2a)(2a)+(3b)(3b)-6ab ) (2a+3b)
et j'obtiens (2a+3b)(2a+3b-6ab) et ce n'est pas possible mon erreur est ou?
-
Rower
- Membre Relatif
- Messages: 357
- Enregistré le: 09 Nov 2006, 18:09
-
 par Rower » 11 Nov 2006, 14:11
par Rower » 11 Nov 2006, 14:11
Tu dois utiliser
(a-b)²=a²+b²-2ab --- identité remarquable que tu dois connaitre
avec les indications de Elsa toup tout s'éclaircit
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 11 Nov 2006, 14:18
par Elsa_toup » 11 Nov 2006, 14:18
Ton erreur est de mal factoriser...
Factoriser, c'est, dans une addition et/ou une soustraction, reconnaitre un terme identique de chaque côté de ces opérations.
Quand tu "factorises" par (2a+3b) à gauche (dans ((2a)(2a)+(3b)(3b)-6ab) ), le problème est que ce (2a+3b) n'apparaît ni dans (2a)(2a), ni dans (3b)(3b), et ni non plus dans 6ab.
Ca ne marche pas donc !
Il faut que tu reconnaisses une identité remarquable dans cette expression.
Passe en revue les 3 que tu connais, et vois laquelle peut convenir.
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 14:21
par Laur » 11 Nov 2006, 14:21
je vous remercie mais regardez ce que j'obtiens::
(4a²-6ab+9b²)(2a+3b)
((2a)²-2fois 2a fois 3b +(3b)²)(2a+2b)
(2a-3b)²(2a+3b) mais ce n'est pas possible je crois que je suis en train de tout melanger
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 11 Nov 2006, 14:23
par Elsa_toup » 11 Nov 2006, 14:23
Ben si, c'est exactement ça ! (avec une petite erreur de frappe dans la ligne intermédiaire : c'est 3b)
Qu'est-ce qui te perturbe ?
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 14:26
par Laur » 11 Nov 2006, 14:26
merci ce qui me perturbe c'est de savoir si c'est vraiment la forme factorise? je ne peu plus factoriser ?
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 11 Nov 2006, 14:29
par Elsa_toup » 11 Nov 2006, 14:29
Ben non, c'est complètement factorisé !
Si tu n'as plus que des produits liant les termes, et si tu ne peux pas factoriser par un nombre (par exemple : (2x-2) = 2(x-1) ), alors tu as terminé!!!
Essaie le 2ème pour voir si tu as compris...
-
Laur
- Membre Naturel
- Messages: 23
- Enregistré le: 26 Avr 2006, 07:25
-
 par Laur » 11 Nov 2006, 14:58
par Laur » 11 Nov 2006, 14:58
d'accord je vous remercie beucoup je vais essayer mais j'ai compris je crois merci beaucoup je vous envoie ma reponse des que j'ai finie merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
