J'ai déjà répondu à la première question :
- Si on approxime le système par un système linéaire, c'est parce qu'on sait parfaitement les résoudre au niveau mathématique donc on détermine sans ambiguïté si le système approximé va être ou pas attractif.
Et si le système linéarisé est attractif, ça prouve que le système non linéarisé l'est aussi,
mais uniquement dans un petit voisinage du point fixe qu'on a étudié (et c'est pas facile du tout de prédire si ce voisinage est "grand" ou pas).
- Si on approxime au voisinage de la position d'équilibre, c'est déjà du fait "concret" que
LA question qu'on se pose, c'est de savoir si tel ou tel
point d'équilibre est attractif ou pas. Et c'est aussi du fait mathématique que l'approximation qu'on fait n'est évidement valable que pour
)
proche d'un certain couple et qu'on veut bien évidement que
)
soit lui aussi proche de
ce même couple pour pouvoir utiliser
la même approximation au rang suivant (*)
- Je comprend pas ce que tu veut dire par "
le système initial est fonctionnel". Si c'est qu'on a une formule (pourie, c'est à dire non linéaire) pour calculer les génération suivantes, on peut certes faire quelques simulations avec un ordi. pour certaines valeurs initiales des données, mais il est tout à fait possible, même après pas mal de simulations qu'on ait "raté" quelque chose (i.e. des cas particuliers de population de départ où l'évolution du système est complètement différente)
- Et de savoir si le système est "attractif" autour d'un point d'équilibre, ça te dit que s'il y a des "petites perturbations" (été plus chaud que d'habitude, maladie pas trop grave d'une des deux espèces, etc...), ça ne va pas changer grand chose : le système reviendra automatiquement (et tout seul...) à son état stable.
Alors que si le système n'est pas attractif (ou peu attractif), ça veut dire qu'il ne restera jamais longtemps dans cet état là : là moindre modification, même minime du système va le faire relativement rapidement basculer dans un état complètement différent... (concrètement parlant, ça veut souvent dire la disparition d'une, voire des deux espèces vu qu'un état qui est toujours stable, ben c'est
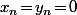
...

)
En bref, ça permet tout bêtement de mesurer la stabilité du système : est-il en équilibre précaire ou bien au contraire archi stable ?
Par exemple : Si la population de poisson/plancton à un endroit donné de la mer est "archi stable", ben ça veut dire qu'on peut en pêcher un assez grand nombre tout les ans sans trop de risque de faire basculer le système.
Si c'est "moyennement stable", ben... gare à la catastrophe...
(*) Là, c'est pas systématiquement vrai : si on entrevoit la possibilité d'un état qui tend vers un truc période sur 2 (ou plus) générations, on peut être conduit à étudier ce qu'il se passe non pas au voisinage d'un point fixe, mais au voisinage d'un point périodique (i.e. qui retombe sur lui même au bout d'un nombre donné d'itérations).

 )
)