Bonjour,
Je bloque complément sur un exercice, j'aurais besoin d'aide, tout est à valeurs dans R.
Soit une matrice A à m lignes et n colonnes et un vecteur b à m coefficients.
Pour tout x à m coefficients, on pose :
E(x) = N(Ax-b)_{2}^{2} (la norme 2 au carré de Ax-b)
Alors il faut montrer que pour a vecteur à m coefficients
E(a) = min E(x) est équivalent à transposé(A) * A * a = transposé(A) * b
Voilà je bloque complètement,
Merci d'avance
Prouver une équivalence à partir de norme
5 messages
- Page 1 sur 1
Re: Prouver une équivalence à partir de norme
Salut,
C'est relativement couillon une fois qu'on a compris un truc "cocon", à savoir que si on a deux vecteur colonne
}\begin{pmatrix}y_1 & y_2& \hdots & y_m\end{pmatrix}\begin{pmatrix}z_1\cr z_2\cr \vdots \cr z_m\end{pmatrix}=y^{T}z)
où désigne le produit scalaire,
désigne le produit scalaire,  la transposée et où dans
la transposée et où dans ) on a identifié un réel et une matrice
on a identifié un réel et une matrice  .
.
Avec ça, on montre facilement le résultat en étudiant la fonction réelle) avec un vecteur
avec un vecteur  fixé.
fixé.
(il suffit de regarder la dérivée de cette fonction en t=0)
P.S. : Pour que ça soit clair au niveau des notation, la transposée de tu la note
tu la note 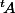 ;
; 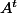 ou
ou 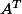 ?
?
C'est relativement couillon une fois qu'on a compris un truc "cocon", à savoir que si on a deux vecteur colonne
où
Avec ça, on montre facilement le résultat en étudiant la fonction réelle
(il suffit de regarder la dérivée de cette fonction en t=0)
P.S. : Pour que ça soit clair au niveau des notation, la transposée de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Prouver une équivalence à partir de norme
Perso j'utilise 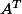
je viens de calculer la dériver, j'obtiens :
 = (Ah)^{T} * ( A * \alpha + A*t*h - b) + (A * \alpha +A*t*h - b)^{T} * (Ah))
et donc en posant t = 0
 = (A*h)^{T}*(A *\alpha - b) + ((A*h)^{T}*(A *\alpha - b))^{T})
après je ne vois pas quoi faire de plus.
je viens de calculer la dériver, j'obtiens :
et donc en posant t = 0
après je ne vois pas quoi faire de plus.
Re: Prouver une équivalence à partir de norme
J'ai l'impression que c'est ça, mais ton écriture (en particulier avec des * pour les produit) est bien lourde.
De plus, tu peut aussi simplifier en utilisant le fait que^T=Y^TX^T) et il te reste à dire aussi que cette quantité doit être nulle quelque soit le vecteur h choisi au départ.
et il te reste à dire aussi que cette quantité doit être nulle quelque soit le vecteur h choisi au départ.
\!=\!E(\alpha\!+\!th)=\|A(\alpha\!+\!t.h)-b\|^2=\|t.Ah+(A\alpha\!-\!b)\|^2=<br />\|t.Ah\|^2+2\!<\!t.Ah\,|\,A\alpha\!-\!b\!>+\|A\alpha\!-\!b\|^2\cr\ \hskip24mm<br />=\|Ah\|^2t^2+2\!<\!Ah\,|\,A\alpha\!-\!b\!>\!t+\|A\alpha\!-\!b\|^2)
Qui est un bête polynôme du second degré en (si le coeff.
(si le coeff.  est non nul).
est non nul).
Si) est effectivement la valeur minimale de
est effectivement la valeur minimale de ) pour tout les
pour tout les 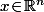 , ça signifie en particulier que
, ça signifie en particulier que \!=\!E(\alpha\!+\!th)\!\geq\!E(\alpha)\!=\!P(0)) pour tout réel
pour tout réel  (1) c'est à dire que le polynôme est minimal pour
(1) c'est à dire que le polynôme est minimal pour  donc que
donc que \!=\!0) c'est à dire que
c'est à dire que  (2) c'est à dire
(2) c'est à dire 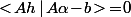 .
.
Or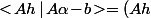^T\!(A\alpha\!-\!b)=h^T\!\big(A^T\!(A\alpha\!-\!b)\big)) et pour que cette matrice
et pour que cette matrice  soit nulle quelque soit le vecteur
soit nulle quelque soit le vecteur  , il faut (et il suffit) que le vecteur
, il faut (et il suffit) que le vecteur) soit nul, c'est à dire que
soit nul, c'est à dire que 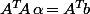 .
.
Réciproquement, si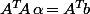 , en remontant la preuve, ça prouve que tout les polynômes du type de
, en remontant la preuve, ça prouve que tout les polynômes du type de  (quelque soit le vecteur
(quelque soit le vecteur  ) vont avoir un minimum en
) vont avoir un minimum en  et ça prouvera bien que
et ça prouvera bien que ) est le minimum de
est le minimum de ) pour tout les
pour tout les 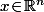 vu que tout les
vu que tout les 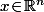 peuvent s'écrire
peuvent s'écrire 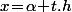 en prenant par exemple
en prenant par exemple 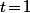 et
et 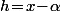 .
.
(1) Attention, écrire un peu comme tu le fait) , ça veut rien dire : le paramètre de
, ça veut rien dire : le paramètre de  c'est un réel et pas une matrice.
c'est un réel et pas une matrice.
(2) Tu peut aussi utiliser le fait bien connu qu'un polynôme admet son minimum en
admet son minimum en 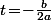 .
.
De plus, tu peut aussi simplifier en utilisant le fait que
Qui est un bête polynôme du second degré en
Si
Or
Réciproquement, si
(1) Attention, écrire un peu comme tu le fait
(2) Tu peut aussi utiliser le fait bien connu qu'un polynôme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
