DM FONCTION INVERSE

[octavia24]

Bonjours, j'ai un DM de math a rendre
Et une des question est la suivante :
"Quelle somme minimal peut on obtenir quand on ajoute un nombre strictement positif et son inverse ? "
J'ai trouvé 2 atteint pour x=1
mais je ne sais pas si cela est juste ni comment le demontrer

Merci de votre aide

[ROXAS300]

Si tu fais le tableau de variation peut-être ?
Ou les limites ? 1/x tend vers 0 donc x+1/x tend vers x donc plus ton x est bas plus x+1/x sera bas
Attends l'avis de personnes plus douées que moi quand même ^^'

[mathelot]

bonsoir,

pour tout x réel x>0




donc 2 est un minorant de f sur

[hdci]

Ou les limites ? 1/x tend vers 0 donc x+1/x tend vers x donc plus ton x est bas plus x+1/x sera bas
Attends l'avis de personnes plus douées que moi quand même ^^'

Attention, on ne peut pas dire que !
est une variable dans l'expression dans la limite, alors qu'à droite de l'égalité on doit avoir un nombre ou l'infini !

[ROXAS300]

Ah je ne savais pas, désolé.

[hdci]

En fait on peut dire que 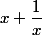est équivalent à au voisinage de l'infini.

Mais ça ce ne sont pas des notions vues au lycée... Et en tout état de cause ne sert pas pour trouver le résultat (1+1=2) car on n'est pas au voisinage de l'infini ici...

[rcompany]

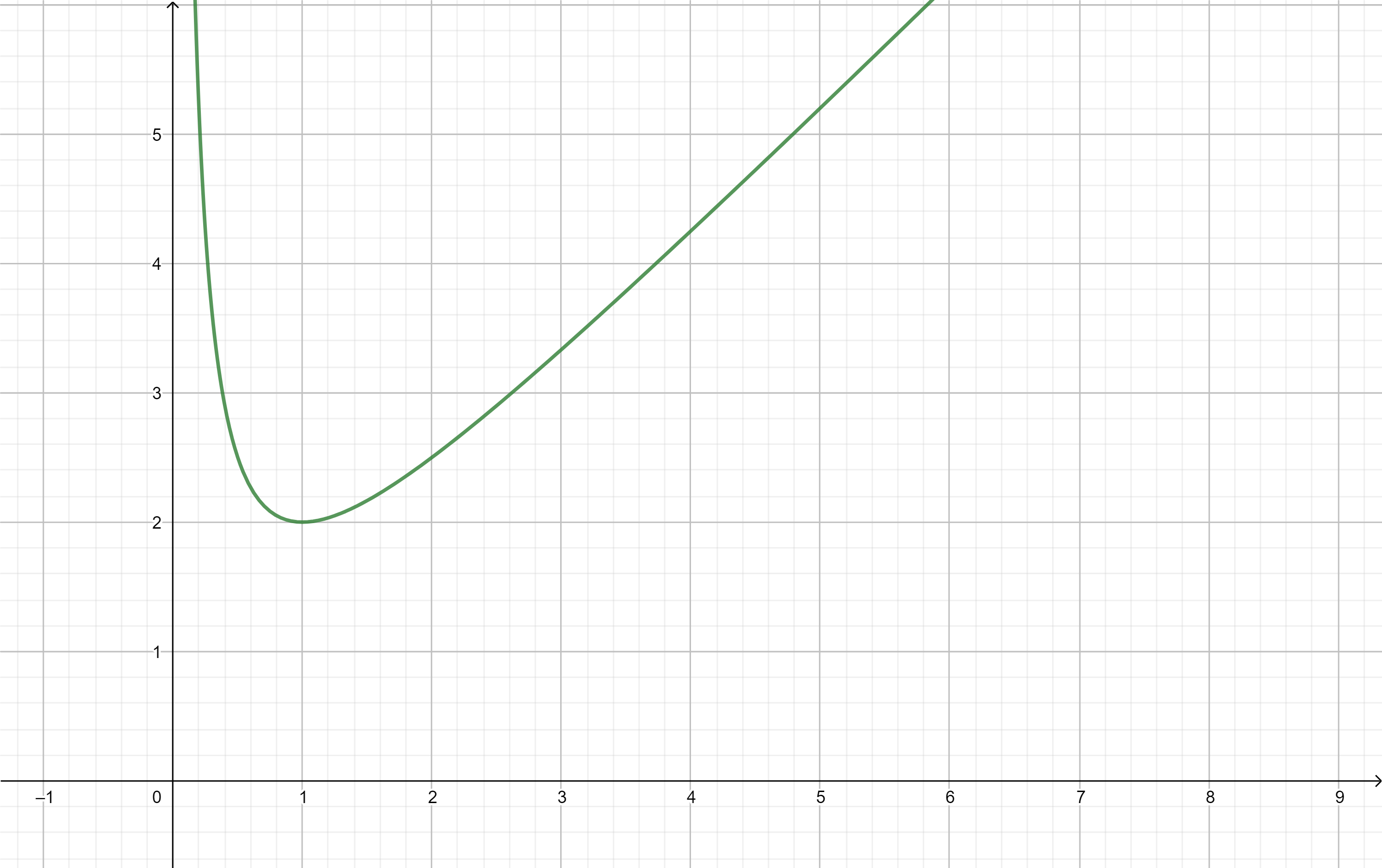
f(x) = 1+1/x; minimum de f(x)?

1. si tu as vu les dérivées, calcule f'(x) et trouve la valeur x0 qui l'annule. f(x) aura donc un extremum en x=x0.
Étudie le sens de variation de f(x) sur ]0;x0] et sur [x0;[ et déduis-en si f(x) admet un minimum ou un maximum en x0

1. si tu n'a pas vu les dérivées, tu vois graphiquement que x=1 donne un minimum. Montre que si x1<x2 sur ]0;1] alors f(x1)>f(x2) donc que f est strictement décroissante sur ]0;1]. Montre ensuite que si x1<x2 sur [1;[ alors f(x1)<f(x2) donc que f est strictement croissante sur [1;[. Donc f(1) est le minimum de f sur [0;[