Bonjour, jai un problème avec des questions de mon exercice que je narrive pas à faire :
1.a)Démontrer que la composition de deux fonctions affines est une fonction affine.
3. Soit la fonction f définie sur [0 ;+õ[ par f(x)=1+(1/1+x)
b) Montrer que (f;)f)(x)=1+(1/(2+1/1+x)),Quelle est lexpression de(f;)f;)f;)f)(x) ?
c) résolvez dans [0 ;+õ[léquation f(x)=x et en déduire f(;)2) ;(f;)f)(;)2)
f) utilisez lencadrement 1;)22 et déterminer un encadrement de ;)2.
merci
Fonctions 1ère
13 messages
- Page 1 sur 1
Bonsoir,
pour la première question, voici comment faire :
tout d'abord, définition d'une fonction affine :
f est une fonction affine s'il existe a et b tels que pour tout x,=ax+b) .
.
Soient f et g deux fonctions affines, alors il existe et
et  tels que pour tout x,
tels que pour tout x, =a_1x+b_1) et il existe
et il existe 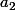 et
et 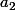 tels que pour tout x,
tels que pour tout x, =a_2x+b_2) .
.
On veut montrer que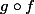 est une fonction affine, c'est-à-dire qu'il existe
est une fonction affine, c'est-à-dire qu'il existe  et
et  tels que pour tout x,
tels que pour tout x, =\alpha x+\beta) .
.
Exprimez) et trouvez
et trouvez  et
et  .
.
pour la première question, voici comment faire :
tout d'abord, définition d'une fonction affine :
f est une fonction affine s'il existe a et b tels que pour tout x,
Soient f et g deux fonctions affines, alors il existe
On veut montrer que
Exprimez
Pour le 1) :
L'équation d'une fonction affine est sous la forme : y = ax + b
Donc tu en prend une : ax + b et une autre cx + d (par exemple).
Ca te fait deux fonctions affines quelconques.
Maintenant avec ça tu fais la composée. Donc tu remplace x de la premiere, par la seconde ? (C'est bien ca la composée ou je me plante ? ^^)
Apres tu calcul le tout, et tu cherche quelque chose sous la force : kx + g
(Avec k et g n'importe quoi sauf quelque chose avec des x)
Tu me comprends?
L'équation d'une fonction affine est sous la forme : y = ax + b
Donc tu en prend une : ax + b et une autre cx + d (par exemple).
Ca te fait deux fonctions affines quelconques.
Maintenant avec ça tu fais la composée. Donc tu remplace x de la premiere, par la seconde ? (C'est bien ca la composée ou je me plante ? ^^)
Apres tu calcul le tout, et tu cherche quelque chose sous la force : kx + g
(Avec k et g n'importe quoi sauf quelque chose avec des x)
Tu me comprends?
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
