Bonjours, je dois donner la fonction dérivées dans la fonction suivante définies sur réelle R, mais je ne sais plus comment faire avec la parenthèse merci.
f(x)=(x^2+x+1)^3
Merci beaucoup.
Fonction dérivées
3 messages
- Page 1 sur 1
Re: Fonction dérivées
par hdci » 29 Oct 2018, 17:20
Bonjour,
Il s'agit ici de dériver une fonction qui s'écrit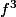
.
Si tu connais la formule de dérivation d'une fonction élevée à une puissance donnée, il suffit de l'appliquer.
Si tu l'as oubliée, tu peux juste remarquer que
et dériver le produit.
En rappelant que'=u'v+v'u)
donc appliqué à 
et 
(puis recommencer pour dériver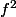 
)
Se souvenir de cette technique, c'est la roue de secours. Le mieux étant bien sûr de connaître les formules, mais passer par la tâche fastidieuse de dériver le produit devra t'inciter à mémoriser la formule adéquate.
Il s'agit ici de dériver une fonction qui s'écrit
Si tu connais la formule de dérivation d'une fonction élevée à une puissance donnée, il suffit de l'appliquer.
Si tu l'as oubliée, tu peux juste remarquer que
En rappelant que
Se souvenir de cette technique, c'est la roue de secours. Le mieux étant bien sûr de connaître les formules, mais passer par la tâche fastidieuse de dériver le produit devra t'inciter à mémoriser la formule adéquate.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :