Montrer que a est un entier
5 messages
- Page 1 sur 1
montrer que a est un entier
montrer que a= ∛(20+14√2) + ∛(20-14√2) est un entier (on utilise (a+b)^3 mais je bloque )
Re: montrer que a est un entier
haithem6 a écrit:montrer que a= ∛(20+14√2) + ∛(20-14√2) est un entier (on utilise (a+b)^3 mais je bloque )
c'est 4! tu résous x² -ax + 2 =0 après avoir remarqué que ∛(20+14√2) * ∛(20-14√2) = 2 et ensuite tu vérifies que les solutions de l'équations correspondent bien à ∛(20+14√2) et ∛(20-14√2)
Re: montrer que a est un entier
on va renommer :
n= ∛(20+14√2) + ∛(20-14√2)
a= ∛(20+14√2)
b= ∛(20-14√2)
(a+b)³= a³ + b³ + 3 a²b +3ab²
après avoir vérifié que tous les membres sous les racines cubiques sont positifs
a²b = (∛(20+14√2))²*∛(20-14√2)
= ∛((20+14√2)²(20-14√2))
=∛((20+14√2)(20+14√2)(20-14√2))
= ∛((20+14√2)(20+14√2)(20-14√2)) <- les deux denier termes sont de la forme (a+b)(a-b)
= ∛((20+14√2)(20²-(14√2)²))
= ∛((20+14√2)8))
=2 ∛(20+14√2)
je te laisse faire les 3 autres termes
soit n³=40+6n
ie : n³-6n-40=0
on peut étudier toute la fonction associée, mais on peut aussi dire que les variations sur le graphe de la fonction imposent une seule et unique solution, et comme n=4 marche, 'est la seule solution.
ouf
n= ∛(20+14√2) + ∛(20-14√2)
a= ∛(20+14√2)
b= ∛(20-14√2)
(a+b)³= a³ + b³ + 3 a²b +3ab²
après avoir vérifié que tous les membres sous les racines cubiques sont positifs
a²b = (∛(20+14√2))²*∛(20-14√2)
= ∛((20+14√2)²(20-14√2))
=∛((20+14√2)(20+14√2)(20-14√2))
= ∛((20+14√2)(20+14√2)(20-14√2)) <- les deux denier termes sont de la forme (a+b)(a-b)
= ∛((20+14√2)(20²-(14√2)²))
= ∛((20+14√2)8))
=2 ∛(20+14√2)
je te laisse faire les 3 autres termes
soit n³=40+6n
ie : n³-6n-40=0
on peut étudier toute la fonction associée, mais on peut aussi dire que les variations sur le graphe de la fonction imposent une seule et unique solution, et comme n=4 marche, 'est la seule solution.
ouf
Re: montrer que a est un entier
Salut,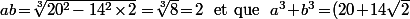\!+\!(20\!-\!14\sqrt{2})\!=\!40) .
.
Ensuite, si on connaît la factorisation de , c'est quasi fini :
, c'est quasi fini :
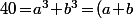(a^2\!-\!ab\!+\!b^2)=(a\!+\!b)\big((a\!+\!b)^2\!-\!3ab\big)=n(n^2\!-\!6))
En terme de "temps de calcul, je pense que c'est judicieux de constater le plus tôt possible quepascal16 a écrit:n= ∛(20+14√2) + ∛(20-14√2)
a= ∛(20+14√2)
b= ∛(20-14√2)
Ensuite, si on connaît la factorisation de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: montrer que a est un entier
c'est clair que foncer bille en tête permet d'arriver au résultat, mais c'est pas forcément le plus court.
En calculant bêtement, c'est là qu'on voit que ab a une forme simple et qu'il est préférable de l'utiliser
En calculant bêtement, c'est là qu'on voit que ab a une forme simple et qu'il est préférable de l'utiliser
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
