Problème : Suite et Fonction

[Yugara]

Bonjour à tous,
Je suis en prépa Bl et souhaitant m'améliorer en maths mon professeur m'a donné un Td de Ece avec des problèmes en plus à essayer de résoudre durant les vacances.
Voici le problème sur lequel je reste bloqué : http://www.noelshack.com/2018-43-4-1540 ... maths1.jpg
(Je suis désolé pour l'hébergeur de l'image mais je n'ai pas bien compris comment poster une image sur ce forum.)

Si cela ne vous gêne pas je vous propose mes réponses pour la première partie : http://www.noelshack.com/2018-43-4-1540 ... maths2.jpg ainsi que http://www.noelshack.com/2018-43-4-1540 ... maths3.jpg
(Encore une fois je suis désolé de poster sur cet hébergeur ! )
Je pense avoir bien compris cette première partie cependant j'ai énormément de mal à commencer la seconde.
Pour la première question j'ai bien compris que ma suite un avait l'air d'avoir pour limite 1 et ainsi pour tout n appartenant à N on aurait bien bien Un appartenant à I mais je ne sais pas comment l'exprimer mathématiquement !
La seconde question ne m'a pas posé de difficultés cependant la troisième beaucoup !
Je ne comprends pas bien si un+1=f(un) alors cela signifierait-il que l'on a un+1= 3un+2/un+4 ?
A partir de ça comment déterminer Un ?


Je vous pose beaucoup de questions et je m'en excuse mais malgré mon faible niveau j'apprécie beaucoup la matière et souhaiterai m'améliorer !

Je vous remercie d'avance pour vos réponses.
Cordialement,

Yugara.

[aviateur]

Tu a démontré que
Donc si
Mais puisque par récurrence on a donc
Maintenant le calcul de qui est demandé montre que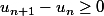
Donc la suite est croissante. Mais elle est majoré par 1 donc elle converge vers un nombre
Mais f est continue sur I donc l=f(l) et d'après une question on sait que l=1.

[aviateur]

**

[jlb]

Salut, pour ton premier document, il y a des soucis de rédaction.
1) la fct f est définie ssi…
5) la courbe de f coupe la droite d'équation y = x...
Sinon, pour la 4), tu balances ton résultat sans expliquer quoique ce soit!! explique au moins un cas.
Et en règle général, précise à chaque fois ce qu'est x: un entier, un réel, un complexe, un réel particulier….
Je regarde la suite.

[jlb]

Oui, tu as bien interprété le " u_(n+1) =f(u_n)", tu peux du coup suivre maintenant les étapes d'Aviateur. Bon courage.

Sinon, c'est une suite définie par récurrence: tu calcules un terme en fonction du précédent et souvent on n'a pas besoin de connaître la formule explicite de u_n pour répondre. Du coup, où, il y a u_n, tu le laisses et tu remplaces u_(n+1) par son expression ( question 3) et tu fais ton calcul comme si u_n est un "x".

[Yugara]

Tu a démontré que
Donc si
Mais puisque par récurrence on a donc
Maintenant le calcul de qui est demandé montre que
Donc la suite est croissante. Mais elle est majoré par 1 donc elle converge vers un nombre
Mais f est continue sur I donc l=f(l) et d'après une question on sait que l=1.

Bonsoir Aviateur,
Je te remercie grandement pour ta réponse !
Si j'ai bien saisi tu me proposes de faire un raisonnement par récurrence non ?
Avec pour initialisation f(I) appartient à l'intervalle I
En hypothèse: si un appartient à I
Et en hérédité alors un+1=f(un) appartient à I
Ai-je raison ?

Pour la question trois j'ai juste à remplacer mes x par un ce qui me donnerait 3un+2/un+4 -un ?
Et par l suite faire le calcul afin de retrouver le résultat demandé n'est-ce pas ?

Je t'en demande beaucoup je suis désolé encore merci pour m'avoir éclairé concernant la question 1!

[Yugara]

Salut, pour ton premier document, il y a des soucis de rédaction.
1) la fct f est définie ssi…
5) la courbe de f coupe la droite d'équation y = x...
Sinon, pour la 4), tu balances ton résultat sans expliquer quoique ce soit!! explique au moins un cas.
Et en règle général, précise à chaque fois ce qu'est x: un entier, un réel, un complexe, un réel particulier….
Je regarde la suite.

Merci pour ces précisions je m'en occupe tout de suite !

[Yugara]

Oui, tu as bien interprété le " u_(n+1) =f(u_n)", tu peux du coup suivre maintenant les étapes d'Aviateur. Bon courage.

Sinon, c'est une suite définie par récurrence: tu calcules un terme en fonction du précédent et souvent on n'a pas besoin de connaître la formule explicite de u_n pour répondre. Du coup, où, il y a u_n, tu le laisses et tu remplaces u_(n+1) par son expression ( question 3) et tu fais ton calcul comme si u_n est un "x".

Merci, ça me rassure d'avoir au moins compris cela.
Pour connaître la monotonie de la suite en réalisant un+1-un je remplace mes X par des un est-ce bien la méthode adapté pour retrouver le résultat ?
J'ai un peu de mal à comprendre comment réaliser le calcul en ne tenant pas compte de la différence entre un et x.

[jlb]

Bonsoir Aviateur,
Je te remercie grandement pour ta réponse !
Si j'ai bien saisi tu me proposes de faire un raisonnement par récurrence non ? oui, tu montres que pour tout n naturel, un appartient à I
Avec pour initialisation f(I) appartient à l'intervalle I Bah non! u_o appartient à I car u_0= ..
En hypothèse: si un appartient à I , f(un) appartient à I Perdu! u_n appartient à I pour un certain n
Et en hérédité alors un+1=f(un) appartient à I car l'image par f de I est incluse dans I et u_n appartient à I par hypothèse
Ai-je raison ? Pas tout à fait du coup!! :D

Pour la question trois j'ai juste à remplacer mes x par un ce qui me donnerait 3un+2/un+4 -un ?
Et par l suite faire le calcul afin de retrouver le résultat demandé n'est-ce pas ? oui! c'est bon et dans ce cas, c'est pas con de développer le truc proposé pour "voir où on va"

Je t'en demande beaucoup je suis désolé encore merci pour m'avoir éclairé concernant la question 1!

[jlb]

Merci, ça me rassure d'avoir au moins compris cela.
Pour connaître la monotonie de la suite en réalisant un+1-un je remplace mes X par des un est-ce bien la méthode adapté pour retrouver le résultat ?
J'ai un peu de mal à comprendre comment réaliser le calcul en ne tenant pas compte de la différence entre un et x.

Je me suis mal fait comprendre: tu écris u_(n+1) - u_n en remplaçant u_(n+1) par (3u_n +2)/(u_n+4) et ensuite tu exprimes le résultat à l'aide des propriétés calculatoires comme si tu devais "simplifier" (3x+2)/(x+2) - x .... ( tu mets au même dénominateur,...) Tu fais comme si u_n c'était un x ou n'importe quelle lettre! cela ne te pose pas de pb quand c'est x ( dérivée,...), cela ne doit pas te poser de pb avec u_n!!

[Yugara]

Merci, ça me rassure d'avoir au moins compris cela.
Pour connaître la monotonie de la suite en réalisant un+1-un je remplace mes X par des un est-ce bien la méthode adapté pour retrouver le résultat ?
J'ai un peu de mal à comprendre comment réaliser le calcul en ne tenant pas compte de la différence entre un et x.

Je me suis mal fait comprendre: tu écris u_(n+1) - u_n en remplaçant u_(n+1) par (3u_n +2)/(u_n+4) et ensuite tu exprimes le résultat à l'aide des propriétés calculatoires comme si tu devais "simplifier" (3x+2)/(x+2) - x .... ( tu mets au même dénominateur,...) Tu fais comme si u_n c'était un x ou n'importe quelle lettre! cela ne te pose pas de pb quand c'est x ( dérivée,...), cela ne doit pas te poser de pb avec u_n!!

Oui j'ai essayé les deux méthodes et j'ai bien le même résultat après factorisation !
Encore merci !

[Yugara]

Bonsoir Aviateur,
Je te remercie grandement pour ta réponse !
Si j'ai bien saisi tu me proposes de faire un raisonnement par récurrence non ? oui, tu montres que pour tout n naturel, un appartient à I
Avec pour initialisation f(I) appartient à l'intervalle I Bah non! u_o appartient à I car u_0= ..
En hypothèse: si un appartient à I , f(un) appartient à I Perdu! u_n appartient à I pour un certain n
Et en hérédité alors un+1=f(un) appartient à I car l'image par f de I est incluse dans I et u_n appartient à I par hypothèse
Ai-je raison ? Pas tout à fait du coup!! :D

Pour la question trois j'ai juste à remplacer mes x par un ce qui me donnerait 3un+2/un+4 -un ?
Et par l suite faire le calcul afin de retrouver le résultat demandé n'est-ce pas ? oui! c'est bon et dans ce cas, c'est pas con de développer le truc proposé pour "voir où on va"

Je t'en demande beaucoup je suis désolé encore merci pour m'avoir éclairé concernant la question 1!

Uhmm oui j'en oublie comment faire un raisonnement par récurrence proprement.On aurait alors

On cherche à montrer que pour tout n appartenant à N on a un appartenant à I
initialisation : uo=o la propriété est vérifié au rang n=0
Hérédité: Si pour tout n appartenant à N on a un appartenant à I
alors on cherche à montrer que pour tout n appartenant à N on a un+1=F(un) appartient à I
Or on a montré qu'auparavant f(I) appartenait bien à I.

Je pense que c'est à cette dernière étape que je bloque !
F(I) appartient bien à I comme nous l'avons vu dans la question 6 le problème c'est que je ne vois pas comment conclure cela.
Edit: Ce que je ne comprends pas c'est ton passage " un+1=f(un) appartenant à I car l'image de I par f est incluse dans I quel est l'impact de cette proposition ? Comment fait-elle avancer le raisonnement ?

Merci encore pour le temps que vous prenez pour me répondre !

[jlb]

Oui, j'en oublie comment faire un raisonnement par récurrence proprement. On aurait alors

On cherche à montrer que pour tout n appartenant à N on a un appartenant à I
initialisation : uo=o la propriété est vérifié au rang n=0
Hérédité: Si pour tout n appartenant à N on a un appartenant à I
alors on cherche à montrer que pour tout n appartenant à N on a un+1=F(un) appartient à I
Or on a montré qu'auparavant f(I) appartenait bien à I. f(I) est inclus dans I !!! attention, f(I) est un ensmble contenu dans un autre

Je pense que c'est à cette dernière étape que je bloque !
F(I) est inclus dans I comme nous l'avons vu dans la question 6 le problème c'est que je ne vois pas comment conclure cela.
Edit: Ce que je ne comprends pas c'est ton passage " un+1=f(un) appartenant à I car l'image de I par f est incluse dans I quel est l'impact de cette proposition ? Comment fait-elle avancer le raisonnement ?

Merci encore pour le temps que vous prenez pour me répondre !

Bah, tu dois montrer que si u_n appartient à I alors u_(n+1) appartient à I! c'est l'hérédité.

DONC: on suppose que u_n appartient à I, comme f envoie I dans I, alors f(u_n) appartient à f(I) donc à I ( c'est là!!) donc u_(n+1)= f(u_n) appatient à I