Logique

[Ilyaskilango]

Salut je suis bloquer Svp aidez moi
On a n appartient à N
Montrer que
(4n+3)/6 n appartient pas à N
Et rac(4n+2018) N appartient pas à N
Et enfin pour tout n appartenant à Z
Montrer que
(8n+2021)/10 n'appartient pas à Z
Svp Svp aidez moi le plus tôt possible

[pascal16]

en démo direct, j'ai pas vu moins de 2 sous-cas, par l'absurde, pas de sous cas :

si (4n+3)/6 est un entier
on a alors l'existence de p tel que
4n+3=6p
soit
n=(6p+3)/4
mais 6p+3 est impair, donc non divisible par 2 ni par 4.
donc p ne peut pas être entier, contradiction

[Ilyaskilango]

Et c'est la même chose pour la 2ème?

[pascal16]

c'est faisable par l'absurde après une descente en 10 étapes du genre
2*(?)=p² implique (?) est pair car p² admet au moins 2² dans sa décomposition en facteur premiers

il y a peut-être plus rapide

[pascal16]

(8n+2021)/10
-> j’étudierais simplement si 8n+2021 peut finir par le chiffre 0.
et rien que par parité...

[Ilyaskilango]

S'il te plait j'ai résolu la 2ème mais est ce que c'est juste
On a par absurde
rac(4n+2018)=s tel que s entier naturel
4n+2018=s^2
n=(s^2-2018)/4
Si s est pair alors s=2k
n=(4k^2-2018)/4
=4(k^2-2018)/4 +2/4
=k^2-2018+1/2 ceci n'appartient pas à N absurde !
Et si s est impair alors s=2k+1
n=(4k^2+4k+1-2018)/4
=[2(k^2+2k+1009)+1]/4 ABSURDE CAR le numérateur est impair dans non divisible ni par 2 ni par 4

Cela est vrai et Stp comment résoudre la dernière

[Ilyaskilango]

Merci pour le dernière je vais voir comment la résoudre par parité

[pascal16]

8n est pair, 8n+1 impair, ne fini par pas 0, non divisible par 10.
(ou : non divisible par 2 donc pas par 10)

[Ben314]

Salut,
Pour le 1), je trouve quand même que tu te fout un peu de la gueule du monde : ça serait ton premier exo. sur l'arithmétique, je dit pas, mais là, on en est on combien-ième que tu met sur le Forum pour avir comme résultat que même le plus "basique de chez basique" tu y arrive pas ?
Bref, pour que 4n+3 soit divisible par 6, ben faudrait au minimum qu'il soit divisible par 2 or 4n+3 est évidement impair.

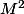Et concernant le deuxième, on peut pas dire non plus que ce soit bien difficile : si (entier) alors donc est pair (sinon serait lui aussi impair), c'est à dire et on a ce qui est évidement impossible vu que 2018 n'est pas divisible par 4.

Et le 3), de nouveau, c'est complètement stupide : pour que 8n+2021 soit divisible par 10, ben faudrait déjà qu'il soit divisible par 2 or il est clairement impair.

Et en résumé, ben ça confirme un truc qui me semble pas particulièrement étonnant, à savoir que de faire que lire les correction qu'on te fait, ben ça fait que tu progresse pas d'un iota et que tout ce que ça va faire, c'est qu'arrivé à l'exam., ben tu aura toujours rien compris au schmilblick (et là, ben je pense pas qu'on pourra le faire à ta place...)

[Ilyaskilango]

Non t'inquiète l'ai lexam de math demain
Et je vais te prouvais que ce forum m'a aider plus que l'ordinaire
Je remercie infiniment tout personne qui ma aider dans ce forum et merci beaucoup à toi ben

[pascal16]

ho surprise, il y avait plus rapide.