Somme double et inégalité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Agouraptor
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2018, 19:54
-
par Agouraptor » 18 Oct 2018, 20:52
Bonjour à tous;
Je fais un exercice sur les sommes avec trois questions et j'aurais besoin d'aide sur la dernière. J'ai surement juste besoin d'un indice sur par quoi commencer :
Soient
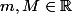
et
.
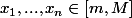
1) J'ai démontré que :
^2) = n \sum_{k = 1}^{n} ({x_k}^2) - (\sum_{k = 1}^{n} (x_k))^2)
2) J'ai ensuite démontré que :
^2) + n \sum_{k = 1}^{n} ((M - x_k)(x_k - m)) = (nM - s)(s - nm))
où
)
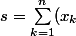3) Maintenant on souhaite déduire de la question précédente l'inégalité suivante, et c'est là ou je bloque :
^2) \leq \frac{n^2(M - m)^2}{2})
En fait c'est surtout l'inégalité qui me pose problème. J'imagine qu'on a pas le droit de partir de l'inégalité puisque c'est ce qu'on tente de démontrer, mais alors, par quoi faut-il commencer ?
-
aviateur
par aviateur » 19 Oct 2018, 05:15
A la question 2, l'expression (nM-s)(s-nm) il faut regarder sa valeur maximale en fonction de s.
J'ai une remarque à faire concernant cette exercice.
Il serait bien de démontrer que la majoration demandée est optimale (ou non).
Modifié en dernier par aviateur le 19 Oct 2018, 11:31, modifié 1 fois.
-
Agouraptor
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2018, 19:54
-
par Agouraptor » 19 Oct 2018, 11:22
Donc, si j'ai bien compris, je pose :
 = (nM - s)(s - nm))
Je trouve donc une valeur maximum de :
^2}{4}) + n(M + m) - n^2mM)
Je vois donc une partie de l'inéquation qui apparait, mais ensuite je ne suis pas sûre de comment continuer.
-
aviateur
par aviateur » 19 Oct 2018, 11:33
Mais il faut simplifier en principe tu dois trouver 1/4*n^2 (M-m)^2
-
aviateur
par aviateur » 19 Oct 2018, 11:36
Et il me semblerait bien que ton maximum est faux. Tu as dû oublier un facteur au terme n(M+m) *
-
Agouraptor
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2018, 19:54
-
par Agouraptor » 19 Oct 2018, 12:18
Oui effectivement, pour le maximum je trouve bien :
^2}{4})
Mais comment est-ce qu'on se ramène à l'inéquation voulu :
^2) \leq \frac{n^2(M + m)^2}{2})
-
Agouraptor
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2018, 19:54
-
par Agouraptor » 19 Oct 2018, 12:57
Ah je crois avoir trouvé :
D'après l'énoncer, on a :
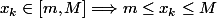
On a donc :
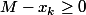
et
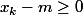
Donc :
(x_k - m)) \geq 0)
Or, d'après ce que tu m'a aider à démontré :
^2) + n \sum_{k = 1}^{n} ((M - x_k)(x_k - m)) \leq \frac{n^2(m + M)^2}{4})
et donc :
^2) \leq \frac{1}{2} \sum_{1 \leq i, j\leq n}^{} ((x_i - x_j)^2) + n \sum_{k = 1}^{n} ((M - x_k)(x_k - m)) \leq \frac{n^2(m + M)^2}{4})
Ou encore :
^2) \leq \frac{n^2(m + M)^2}{4})
et finalement :
^2) \leq \frac{n^2(m + M)^2}{2})
Est-ce correct ?
-
aviateur
par aviateur » 19 Oct 2018, 15:31
Ici j'ai pas le temps de regarder ton dernier long message je le ferai éventuellement tout à l'heure mais pour le majorant c'est pas ça dans le carré c'est pas M+m mais M-m
D'ailleurs j'ai dit ce que tu devais trouver
-
Agouraptor
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2018, 19:54
-
par Agouraptor » 19 Oct 2018, 15:48
Oui, effectivement, désoler, c'est bien un M-m, heureusement je ne pense que cela ne change pas mon raisonnement dans mon dernier message. Merci pour ton aide.
-
aviateur
par aviateur » 19 Oct 2018, 17:40
oui alors c'est ça en corrigeant le signe
-
Agouraptor
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Oct 2018, 19:54
-
par Agouraptor » 19 Oct 2018, 18:00
Parfait, merci beaucoup.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
