Limite en +oo
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
qaterio
- Membre Relatif
- Messages: 288
- Enregistré le: 22 Aoû 2018, 18:55
-
 par qaterio » 11 Oct 2018, 12:23
par qaterio » 11 Oct 2018, 12:23
Bonjour,
On sait que
)
est équivalent à
)
(en +oo),
alors je me posais la question de comment comment connaître la limite de
-ln(x))
en +oo ? J'imagine que c'est pas nécessairement 0.
Merci d'avance.
(c'est juste une question que je me pose pour apprendre des astuces en mathématiques, si ça se trouve, c'est peut-être assez délicat à calculer, j'en ai aucune idée)
Modifié en dernier par
qaterio le 11 Oct 2018, 12:30, modifié 2 fois.
-
aviateur
 par aviateur » 11 Oct 2018, 12:25
par aviateur » 11 Oct 2018, 12:25
Tu peux écrire correctement ta fonction:
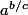
ça s'écrit a^{b/c}
sinon on comprend rien.
-
qaterio
- Membre Relatif
- Messages: 288
- Enregistré le: 22 Aoû 2018, 18:55
-
 par qaterio » 11 Oct 2018, 12:26
par qaterio » 11 Oct 2018, 12:26
Merci.
-
aviateur
 par aviateur » 11 Oct 2018, 12:32
par aviateur » 11 Oct 2018, 12:32
La limite est 0. En effet
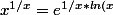}=)
Mais u=ln(x)/x tend vers 0 dq x tens vers + infini alors on utilise e^u=1+u+u^2/2+o(u^2)
donc
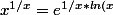}=1+log(x)/x +1/2 (+log(x)/x )^2+o((ln(x)/x)^2))
et alors
-log(x)=x (1+log(x)/x +1/2 (log(x)/x)^2+o((ln(x)/x)^2)-1)-log(x)=1/2 log(x)^2/x +o(...))
....--->0
Modifié en dernier par aviateur le 11 Oct 2018, 12:39, modifié 1 fois.
-
qaterio
- Membre Relatif
- Messages: 288
- Enregistré le: 22 Aoû 2018, 18:55
-
 par qaterio » 11 Oct 2018, 12:38
par qaterio » 11 Oct 2018, 12:38
Je te remercie.
-
aviateur
 par aviateur » 11 Oct 2018, 12:41
par aviateur » 11 Oct 2018, 12:41
qaterio a écrit:'est peut-être assez délicat à calculer,
Non en principe ça doit pas poser de problème cela ne fait intervenir que des fonctions usuelles.
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 11 Oct 2018, 12:41
par Landstockman » 11 Oct 2018, 12:41
Tu as déjà vu le chapitre sur les développements limités qaterio ?
-
qaterio
- Membre Relatif
- Messages: 288
- Enregistré le: 22 Aoû 2018, 18:55
-
 par qaterio » 11 Oct 2018, 12:56
par qaterio » 11 Oct 2018, 12:56
Oui mais c'est très récent, et on ne l'a pas vu en maths, mais en physique, on a juste la formule générale pour trouver les développements limités et on nous a donné les Dév. Lim. de exp. cos. et sin.
-
Landstockman
- Membre Relatif
- Messages: 188
- Enregistré le: 11 Aoû 2015, 07:22
-
 par Landstockman » 11 Oct 2018, 13:04
par Landstockman » 11 Oct 2018, 13:04
Ah ok
Bon ici tu n'as pas besoin de plus tant mieux

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
