Bonjour
Je connais pas vraiment les séries de Puiseux mais on devine un peu ce qu'il se passe. Si j'ai bien compris
si 0 est d'ordre 3, on aurait du

Par contre ce que je veux dire c'est qu'il y a dérivabilité lorsque la dimension du noyau = l'ordre de multiplicité de 0.
Par exemple si on prend 0 de multiplicité 2 et dim Ker M_0= 2 aussi.
Alors je dans ce cas la matrice M(z) admet un "groupe" deux 2 valeurs propres
)
et
)
convergeant vers 0 mais de plus elles sont dérivables.
De plus, on peut montrer que
)
et
)
correspondent aux valeurs propres de l'opérateur
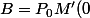P_0)
où
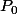
est l'opérateur de projection sur

défini par
^{-1} d \xi)
(

étant un cercle qui entoure 0 et qui ne contient pas les autres valeurs propres de

)
On vérifier cela sur un exemple:
Soit
=\left(<br />\begin{array}{ccc}<br />\sin(z) & z & z \\ z & 0 & z \\ z & z & 2+z<br />\end{array}<br />\right))
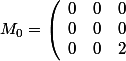)
après calculs on trouve que les valeurs propres de B sont
,\frac{1}{2} \left(1-\sqrt{5}\right)\right\}\approx \{1.61803,-0.618034\}.)
Bien sûr, calculer les valeurs propres de M(z) c'est pas une chose facile mais numériquement on calcule

valeurs propres de M(z) pour des valeurs de z petites
Cela donne
z=1/10 : (21.1021,1.51981,-0.623561)
z=1/100: (201.01,1.60852,-0.618564)
z=1/1000 : (2001.,1.61709,-0.618087)
z=1/100000 : (200001.,1.61802,-0.618035)
Pour les détails du calcul je le laisse en énigme.
Mais pour la démo il y a du boulot.
Modifié en dernier par aviateur le 10 Oct 2018, 15:56, modifié 2 fois.
un corps,
et
(donc
)).