Absurde
5 messages
- Page 1 sur 1
Re: Absurde
Salut, raisonnons par l'absurde.
Suppose que c'est un rationnel.
Alors son carré est aussi rationnel,
(Racine(2)-racine(3))^2=5-2racine(6)
Donc le nombre [ (racine(2)-racine(3))^2-5]/(-2) est un rationnel... donc racine(6) est rationnel.
Absurde.
Suppose que c'est un rationnel.
Alors son carré est aussi rationnel,
(Racine(2)-racine(3))^2=5-2racine(6)
Donc le nombre [ (racine(2)-racine(3))^2-5]/(-2) est un rationnel... donc racine(6) est rationnel.
Absurde.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Absurde
Lostounet a procédé par l'absurde :
Il suppose que racine(2)-racine(3) est un rationnel, il montre qu'il y a une incohérence, et donc que cette supposition est fausse.
Commençons par remarquer que si on multiplie un nombre rationnel r par lui même, le résultat (cad r^2) est toujours rationnel. Donc si racine(2)-racine(3) est rationnel,alors^2=5-2\sqrt 6) est rationnel. Donc on aurait
est rationnel. Donc on aurait  rationnel. Sauf que si on enlève
rationnel. Sauf que si on enlève  c'est toujours un rationnel. On a alors
c'est toujours un rationnel. On a alors  rationnel. On divise par -2, ça reste rationnel, donc
rationnel. On divise par -2, ça reste rationnel, donc 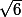 . Mais ça c'est faux, c'est un résultat connu. Si tu ne sais pas le montrer, tu peux chercher comment montrer que
. Mais ça c'est faux, c'est un résultat connu. Si tu ne sais pas le montrer, tu peux chercher comment montrer que  n'est pas rationnel, c'est sensiblement la même chose.
n'est pas rationnel, c'est sensiblement la même chose.
On a donc une incohérence, d'où racine(2)-racine(3) n'est pas rationnel
Il suppose que racine(2)-racine(3) est un rationnel, il montre qu'il y a une incohérence, et donc que cette supposition est fausse.
Commençons par remarquer que si on multiplie un nombre rationnel r par lui même, le résultat (cad r^2) est toujours rationnel. Donc si racine(2)-racine(3) est rationnel,alors
On a donc une incohérence, d'où racine(2)-racine(3) n'est pas rationnel
Re: Absurde
Bon ... commence par rappeler:
1) C'est quoi la définition d'un nombre rationnel?
D'un irrationnel?
2) Si un nombre est rationnel, que dire de son carré?
3) Est-ce que racine de 6 est un rationnel ou non? Comment le montrer?
Ps attention à ne pas commettre l'erreur qui consiste à montrer que racine 2 et racine 3 sont irrationnels et d'en conclure que leur différence l'est aussi.
1) C'est quoi la définition d'un nombre rationnel?
D'un irrationnel?
2) Si un nombre est rationnel, que dire de son carré?
3) Est-ce que racine de 6 est un rationnel ou non? Comment le montrer?
Ps attention à ne pas commettre l'erreur qui consiste à montrer que racine 2 et racine 3 sont irrationnels et d'en conclure que leur différence l'est aussi.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
