Comparaison

[stef78]

Bonjour

On devait comparer ces f(x) et g(x)

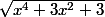
f(x)= et g(x)=x²

Voila comment la prof a fait:

>
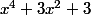
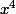
donc :




je voudrais savoir si c'est parce que
= x² ?

Si c'est ca pouvez vous m'inventer un autre petit exemple pour voir si j'ai compris?

merci!

[Imod]

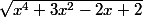
En voilà un , un peu plus difficile , comparer : et .

Imod

[Zebulon]

Bonsoir,

On devait comparer ces f(x) et g(x)
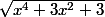
f(x)= et g(x)=x²
Voila comment la prof a fait:
>
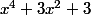
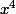
donc :

je voudrais savoir si c'est parce que
= x² ?

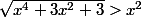
non, c'est parce que la fonction racine carrée est croissante sur . On en déduit que , c'est-à-dire que f(x)>g(x).

Si c'est ca pouvez vous m'inventer un autre petit exemple pour voir si j'ai compris?

Cool ! Un élève qui réclame des exercices ! :ptdr:
Comparez f et g définies par :
et g(x)=1.

[stef78]

Ok,merci

deja pour :
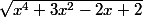
et .

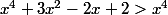
+ 1²

>
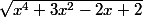
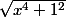
donc > x²+1

mais je suis pas sur que l'on puisse faire ca je crois pas donc je bloque un peu

[Imod]

Il y a une erreur dans le développement de ton second membre : c'est un produit remarquable (a+b)^2 = ...

Imod

[stef78]

a OK

x²+1= (x+1)² = x² + 2x + 1

donc
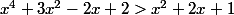
Comment demontrer apres ca?

Peut on faire :



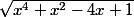
Or > 0

donc f(x) >g(x)

C'est possible?

[Imod]

Attention : .

Imod

[stef78]

Mais pourquoi mettons nous tout au carré?

[Imod]

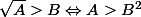
Si A et B sont positifs : . L'intérêt est d'avoir une inégalité sans radicaux .

Imod

[stef78]

Aaaa Ok merci

Donc

>

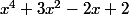
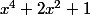
Soit


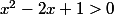
et donc (x-1)²>0

Par consequent f(x) > g(x)

[Imod]

Et voilà :++: . Bien sûr , pour être tout à fait correct ,il faudrait vérifier que les deux membres de départ sont toujours positifs :we:

Imod

PS: l'exercice de Zebulon n'est pas inintéressant ( loin de là ) mais attention à ne pas compliquer inutilement .