Analyse

[blackpoetry]

bonsoir
svp comment montrer que pour tous réels a et b et c on a :

b²c²+c²a²+a²b² ≥ abc(a+b+c)

[Lostounet]

bonsoir
svp comment montrer que pour tous réels a et b et c on a :

b²c²+c²a²+a²b² ≥ abc(a+b+c)

En posant:
F(c)= b²c²+c²a²+a²b² - abc(a+b+c)
= (a^2+b^2 - ab)c^2 +( - a^2b - ab^2)c + a^2b^2

Qui a pour discriminant:
Delta = ( - a^2b - ab^2)^2-4(a^2+b^2-ab)(a^2b^2)

= -3a^2b^2 (a-b)^2

Qui est toujours négatif (sauf en a=b où il est nul).

Reste à étudier le signe de a^2+b^2-ab (terme dominant) pour conclure.

[Ben314]

Salut, il y a des tas et des tas de méthodes plus ou moins astucieuses et plus ou moins rapides.
Du pas très astucieux, mais pas super long, ça peut consister à dire que :
- Si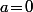 , le résultat est évident.
- Sinon, on peut tout diviser par et, en posant et , ce qu'il faut démontrer, c'est que .
Vu comme polynôme du second degré en , le discriminant du trinôme est

Donc le trinôme est de signe constant, à savoir celui du coefficient en qui est (car de discriminant =-3<0).

EDIT : Idem le post de Lostounet sauf que j'ai commencé par virer une variable de fait de l'homogénéité.

[Ben314]

Sinon, dans le plus subtil, y'a ça :

[blackpoetry]

Merci j'ai trouvé une simple méthode;

on sait que x²+y²≥2xy

alors: b²+a²≥2ab
( c²≥0) b²c²+c²a²≥2abc² 1

de meme c²+a²≥2ac
ce qui implique que b²c²+a²b²≥2acb² 2

et aussi b²+c²≥2bc
donc a²b²+a²c²≥2a²bc 3

la somme de 1,2 et 3 membre par membre nous donne:

2b²c²+2c²a²+2a²b²≥2abc²+2acb²+2a²bc

d'ou b²c²+c²a²+a²b²≥abc(a+b+c)

[Lostounet]

C'est un peu ce qu'a écrit Ben non?