[MPSI] Complexe

[acrobate23]

Bonjour, j'ai un exercice qui est le suivant:

Soit p ∈ C* et q ∈ C. On se propose de résoudre l'équation d'inconnu z ∈ C.
(E): z^3 + pz + q = 0

Pour cela on introduit le système auxiliaire (S) d'inconnu (u,v) ∈ C^2 et l'équation du second degré (E')

(S): 3uv = -p et u^3 + v^3 = -q

(E'): z^2 + qz - ((p^3)/27)

Questions:
1. a) Soit (u,v) ∈ C^2 solution de (S). Montrer que z = u + v est solution de (E)
J'ai réussi cette question en remplaçant z par u+v dans (E) et avec le système S j'arrive bien à 0

b) Réciproquement soit z ∈ C une solution de (E):
- Établir qu'il existe (u,v) ∈ C^2 tel que le système suivant soit vérifié à savoir u + v = z et 3uv = -p
Alors je ne sais pas trop comment justifier cela car la première équation résulte de la première question mais pour la deuxième je ne sais pas trop comment m'y prendre

-Montrer qu'alors (u,v) est solution de S
La je ne comprend absolument pas la question comment passer du système précédant à S

Voila l'exercice est encore plus long mais je me dis que si j'arrive déjà ces premières questions ça pourra peut être me débloquer pour la suite
Merci d'avance pour vos réponses

[Ben314]

Salut,

b) Réciproquement soit z ∈ C une solution de (E):
- Établir qu'il existe (u,v) ∈ C^2 tel que le système suivant soit vérifié à savoir u + v = z et 3uv = -p
Alors je ne sais pas trop comment justifier cela car la première équation résulte de la première question mais pour la deuxième je ne sais pas trop comment m'y prendre.

Il y a deux "début" possibles :
- Soit tu as déjà vu qu'étant donné deux "nombres" (réels ou complexes) et , de chercher les nombres et 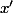de somme et de produit , ça revient à chercher les solution de l'équation
- Soit tu part de zéro en écrivant que tes conditions peuvent se réécrire sous la forme v=z-u et 3u(z-u)=-p puis que la deuxième condition est en fait une équation du second degré (en u bien sûr) (et une fois u trouvé, la première condition te donnera évidement la valeur de v)
Dans les deux cas, tu termine en disant qu'une équation du second degré (à coeff. complexes) possède toujours au moins une solution dans C (et tu es pas obligé de calculer les solutions vu qu'on te demande juste d'expliquer pourquoi on est sûr qu'il y existe u et v tel que ... mais qu'on te demande pas de donner explicitement des valeurs de u et de v)

Pour la troisième question, ce qu'on te demande de montrer, c'est que si tu as des complexes tels que :

Alors le système (S) est forcément vérifié, c'est à dire que tu as forcément et .
Et comme la première égalité fait déjà parti des hypothèses, ça signifie que le seul truc que tu as à démontrer, c'est que les 3 hypothèses impliquent que .
Il y a des tas de façons de procéder. Par exemple d'utiliser pour écrire 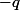en fonction de et , puis d'utiliser et pour écrire et en fonction de et ce qui au final te donnera 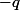en fonction de et .