Suite géométrique

[Rory89]

Bonjour...

je fais appel à vous pour une raison assez bête...

Je vous explique mon exercice, et où j'en suis :
"
On considère la suite (Un) de premier terme u0 = 1 et telle que : Un+1 = 5Un+8
"
J'ai une question intermédiaire, mais elles sont a traiter indépendamment selon l'énoncé, donc aucune importance.
"
On considère la suite (Vn) définie par Vn = Un+2
"
J'ai donc calculé les premiers termes de la suite, et vu qu'elle semblait être géométrique de raison 5 (3;15;75;...)
Pour le prouver, je dois faire Vn+1/Vn, et là... ça bloque !
Je me retrouve donc avec (5Un+10)/(5Un-1+10) Et je ne sais pas quoi faire...
Je sais que je dois trouver 5, mais à part simplifier par 5... Je ne vois pas comment je peux me débarrasser de mon Un et Un-1...

Merci d'avance de votre potentielle aide...

Rory89.

[hdci]

Bonjour,

Je me retrouve donc avec (5Un+10)/(5Un-1+10) Et je ne sais pas quoi faire...

Etes-vous sûr que c'est ?

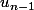Remplacez bien par sa définition et comme vous calculez , vous devez écrire en fonction de au numérateur, et vous allez voir une simplification apparaître.

Attention : pour écrire une fraction, il faut être sûr que le dénominateur n'est pas nul, il vous faut donc avant tout montrer que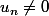 pour tout n.

[Rory89]

Je vient de montrer que pour tout n Un != 0

Cependant, je ne comprends pas mon erreur... je suppose qu'elle est dans l'expression de Vn+1...
Vn+1 = Un+1+2 ?

[Rory89]

(Désolé du doubles postes je ne sais pas si c'est autorisé...)

J'ai essayé d'exprimer Vn+1 par 5(5Un+8)+8 mais je me retrouve à la fin avec (5Un+10)/(Un+2) donc ça ne m'aide pas plus...

[Ben314]

Salut,
Perso., ce que je comprend pas bien, c'est ce que tu bricole avec ton Vn+1/Vn (mais, bon, d'un autre coté, la façon dont on présente les chose au Lycée, ça fait un moment que j'ai arrèté de chercher à comprendre où était la logique...)
Ton énoncé, il te donne :
(1) L'expression de en fonction de :
(2) L'expression de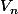 en fonction de :
(3) Qui donne aussi l'expression de en fonction de : (car la formule est valable pour tout n)
(4) Et tu en déduit aussi de façon immédiate l'expression de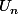 en fonction de :
Et tout ça, ça me semble quand même être "d'une simplicité déconcertante" et ça permet évidement de conclure vu que (3) puis (1) puis (4) te donne en fonction de .

[Rory89]

Désolé du retard...
Merci Ben314 pour tes explications... Le problème c'est que je fais un blocage sur ça... Je ne sais pas, bref.

J'ai donc essayer d'exprimer :
Cela me donne :
Ce qui au final me donne :

Je suppose donc que je me suis encore tromper quelque part, car je ne vois pas comment finir avec ma constante 5 à la fin...

[Sa Majesté]

Et si tu factorisais ?
Ne vois-tu pas un facteur commun ?

[Rory89]

Autant pour moi... Désolé c'était plus qu'évident là...

Merci de votre aide !

[Sa Majesté]

Comme disait mon prof de maths de terminale : "Ordre et méthode".
Je me permets d'ajouter : "Expérience".

[Rory89]

Oui...

Désolé je reviens encore car j'ai encore une raison à trouver...

J'ai fait toutes les étapes de la récurrence avant etc...

C'est toujours le même problème qu'avant en soit :
On définie ensuite une Suite V :

j'ai donc écrit :

Sauf que si je remplace, je tombe sur :

Et là, je ne vois pas comment la réduire, même en factorisant...

(je dois trouver la raison q = )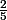

merci....

[Lostounet]

Salut,

Si tu as du mal en calcul, c'est une mauvaise idée de commencer ton calcul par Vn+1/Vn... tu te retrouveras systématiquement bloqué vu que tu ne sais pas encore bien factoriser...


Essaye plutôt d'écrire Vn+1=.....=q*Vn

En gros Vn+1=(Un+1-5)= 2/5Un + 3 - 5= 2/5Un -2
= 2/5*(Un - ???)
=

[Rory89]

.... Effectivement j'avais pas vu que je pouvais simplifier par 2/5 c'est pourtant évident après l'avoir vu... Il me reste plus qu'à simplifier par et j'ai mon 2/5...

Merci beaucoup....