Not f(x)=y but f(x,y)=expr:?

[Intelego]

Bonjours,

Le mathématique ne me laisse pas un jour sans être surpris.

Par exemple aujourd’hui j’ai découvert une notation qui m’a laissé complètement perplexe.

f(x,y)= et puis une expression comme dans les deux documents ci-joint.

Je connais f(x)= et je suis entraîné à écrire ensuite y.

Mais f(y)= c’est déjà difficile à imaginer pour moi mais f(x,y)=, alors je ne vois sincèrement pas quel peut-être la représentation du graph ainsi énoncé. Ni comment construire une courbe.
Si un logiciel existait sous quelle forme de données lui proposer pareil écriture ?

Problème

Solution

Le problème est peut-être plus simple qu’il ne semble. Et en quelques mots, facile à expliquer ?

Cordialement,

Intelego.

[Ben314]

Salut,
Ben pourtant, des trucs du même style, tu en as vu depuis (au moins) le début du collège.
Par exemple, la surface d'un rectangle, c'est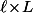 donc c'est un truc qui, pour être calculé, demande la connaissances de DEUX valeur numérique et pas d'une seule, donc c'est... une fonction de DEUX variables... que l'on peut écrire si on veut .
Et de façon bien plus générale, en math. (et en physique, et en chimie et... dans la vie de tout les jours...), on manipule extrêmement souvent des quantités (numérique ou pas) qui dépendent d'autres (au pluriels) quantités, c'est à dire qui varient en fonction de ces autres quantités (d'où le terme consacré de "fonction" en mathématique).

Ensuite, un autre truc à bien comprendre, c'est que la notion de "graphe" d'une fonction, en tant que partie du plan (i.e. de dessin sur une feuille ou un écran), c'est un truc qui ne s'applique qu'à un cas très très particulier de fonction, à savoir celles qui, à une (unique) valeur numérique (= un réel) associe une (unique) autre valeur numérique, mais qu'il y a des tonnes d'autres fonction intéressantes à étudier qui elles ne possèdent pas de graphe (en tout cas pas au sens d'un dessin dans le plan)
Parmi ces autres fonctions tu as forcément déjà vu, les translation (qui à un point associent un autre point), la fonction qui à un complexe associe son module, les différentes fonction permettant de calculer un volume (par exemple f(R,h)=pi.R^2.h pour un cylindre), la fonction qui, à un mot du dictionnaire associe son nombre de lettres, la fonction qui à un objet associe sa couleur, etc, etc, etc...
Dans chacun de ces cas, est-ce qui que ce soit t'a parlé du graphe de ces fonctions ?
Est-ce que tu ne t'es jamais posé la question du "pourquoi" on ne parlait pas du graphe d'une translation ?

Et là, concernant la fonction f de ton exercice, de ce que j'arrive à lire (c'est illisible, surtout avec le bleu par dessus) j'ai l'impression qu'il s'agit d'une fonction qui, à deux entiers associe un entier donc, évidement, la notion de "graphe" au sens usuel (d'une partie du plan R^2) n'a pas le moindre sens dans ce contexte.

[Intelego]

Bonjour,


À chaque fois avec les mathématiques, on passe d’un silence abyssal à une représentation complète, autonome, fonctionnelle.
Et on se demande pourquoi le vrai est si proche et soi du vrai, si lointain ?

Je pense que ce que vous avez dit est assez clair mais comme les copies d'écrans vous ont parues floues, je les renvoient plus nettes.

problème

solution

Merci,


Intelego