Probabilité
39 messages
- Page 1 sur 2 - 1, 2
probabilité
l'exercice est :
6 A propos des pi`eces d´efectueuses
On consid`ere un lot de 10 pi`eces dont la moiti´e sont d´efectueuses. On pr´el`eve sans remise un ´echantillon de taille
3.
1. Quelle est la probabilit´e que l’´echantillon ne comprenne aucune pi`ece d´efectueuse ?
2. Quelle est la probabilit´e pour que le deuxi`eme pi`ece pr´elev´ee ne soit pas d´efectueuse ?
ma reponse est :
1.E:" l’´echantillon ne comprenne aucune pi`ece d´efectueuse"
p(E)=1-1/2 + 4/10 +3/10 =0.94
2.B:"le deuxi`eme pi`ece pr´elev´ee n'est pas d´efectueuse"
p(B)=4/10 et en ce point je touve une difficulte j'ai oublier la logique de proba dans ce cas d' exmple puisque c'est la 1ere semaine apres la vacance j'ai oublier tout hhhhhhh une petite rappelle svp
6 A propos des pi`eces d´efectueuses
On consid`ere un lot de 10 pi`eces dont la moiti´e sont d´efectueuses. On pr´el`eve sans remise un ´echantillon de taille
3.
1. Quelle est la probabilit´e que l’´echantillon ne comprenne aucune pi`ece d´efectueuse ?
2. Quelle est la probabilit´e pour que le deuxi`eme pi`ece pr´elev´ee ne soit pas d´efectueuse ?
ma reponse est :
1.E:" l’´echantillon ne comprenne aucune pi`ece d´efectueuse"
p(E)=1-1/2 + 4/10 +3/10 =0.94
2.B:"le deuxi`eme pi`ece pr´elev´ee n'est pas d´efectueuse"
p(B)=4/10 et en ce point je touve une difficulte j'ai oublier la logique de proba dans ce cas d' exmple puisque c'est la 1ere semaine apres la vacance j'ai oublier tout hhhhhhh une petite rappelle svp
Re: probabilité
Tu as surtout oublié de dire bonjour et d'éviter de faire trop de fautes.
Pour ta réponse 1. je ne comprends pas d'où viennent tes calculs!!!
A mon avis tu devrais commencer par dire "combien tu as de tirages possibles"
Et puis combien de tirages vont te donner aucune pièces défectueuses (nbre de cas favorables on dit je crois??)
Pour ta réponse 1. je ne comprends pas d'où viennent tes calculs!!!
A mon avis tu devrais commencer par dire "combien tu as de tirages possibles"
Et puis combien de tirages vont te donner aucune pièces défectueuses (nbre de cas favorables on dit je crois??)
Re: probabilité
Salut,
Peut-être qu'au niveau "supérieur", il faudrait commencer à utiliser un peu... ta cervelle...
Est-ce que vraiment, tu pense que la proba de tirer trois pièces non défectueuse puisse être de 0,94 sachant que la première pièce que tu tire, y'a déjà une chance sur deux qu'elle soit défectueuse ?



Peut-être qu'au niveau "supérieur", il faudrait commencer à utiliser un peu... ta cervelle...
Est-ce que vraiment, tu pense que la proba de tirer trois pièces non défectueuse puisse être de 0,94 sachant que la première pièce que tu tire, y'a déjà une chance sur deux qu'elle soit défectueuse ?




Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: probabilité
desole pour les fautes et d'oublier de dire bonjour
j'ai fait des fautes lorsque j'ai copier l' exercice p(E)=1-1/2 + 4/10 +3/10 =0.94
c'est en faite p(E)=1/2 * 4/10 *3/10 =0.06
j'ai calculé la proba d'avoire les 3 pièces non d´efectueuses c'est 1/2 : la proba que la 1ere est non d´efectueuses
4/10 : la 2eme non d´efectueuses
3/10:la 3eme non d´efectueuses
puisque c'est un tirage sans remise de 3 pièce parmis 10
j'ai fait des fautes lorsque j'ai copier l' exercice p(E)=1-1/2 + 4/10 +3/10 =0.94
c'est en faite p(E)=1/2 * 4/10 *3/10 =0.06
j'ai calculé la proba d'avoire les 3 pièces non d´efectueuses c'est 1/2 : la proba que la 1ere est non d´efectueuses
4/10 : la 2eme non d´efectueuses
3/10:la 3eme non d´efectueuses
puisque c'est un tirage sans remise de 3 pièce parmis 10
Re: probabilité
Bon j'ai pas fait le calcul mais je crois que 0.06 c'est pas ça.
Du point de vue raisonnement ça ne colle pas.
Si je raisonne comme toi sur un exemple + simple
Par exemple j'ai 3 pièces (D pour défectueuses ) et je tire deux pièces sans remises et cherche la proba que les 2 pieces soient bonnes.
(D pour défectueuses ) et je tire deux pièces sans remises et cherche la proba que les 2 pieces soient bonnes.
Avec ton raisonnement ça fait p=1/3*1/2=1/6.
alors que le nombre de tirages possibles est 3 (B_1,B_2 ) (B_1, D) et (B_2,D)
alors qu'il n'y a qu'un cas favorables (B_1,B_2 ) donc p=1/3.
Du point de vue raisonnement ça ne colle pas.
Si je raisonne comme toi sur un exemple + simple
Par exemple j'ai 3 pièces
Avec ton raisonnement ça fait p=1/3*1/2=1/6.
alors que le nombre de tirages possibles est 3 (B_1,B_2 ) (B_1, D) et (B_2,D)
alors qu'il n'y a qu'un cas favorables (B_1,B_2 ) donc p=1/3.
Re: probabilité
peut etre si je multiplie 1/6 par2 qui est le nombre de permutation entre B_1 et B_2 ça devient correcte non ?
Re: probabilité
C'est plutôt dangereux de faire d'un raisonnement faux une multiplication hasardeuse pour pour arriver au bon résultat.
Il n'y a qu'une possibilité c'est de comprendre le petit calcul de proba que j'ai donné en exemple car c'est ce raisonnement que tu dois appliquer à ton exercice.
Au demeurant il s'agit de dénombrement : savoir que le nombre de sous ensembles de p éléments dans un ensemble de n éléments c'est binomial(n,p) ( )
)
Il n'y a qu'une possibilité c'est de comprendre le petit calcul de proba que j'ai donné en exemple car c'est ce raisonnement que tu dois appliquer à ton exercice.
Au demeurant il s'agit de dénombrement : savoir que le nombre de sous ensembles de p éléments dans un ensemble de n éléments c'est binomial(n,p) (
Re: probabilité
euh juste que cela doit marcher aussi comme le faisait ayabaklouti,
c'est juste qu' après le bon 5/10 ben c'est le 4/9 et pas 4/10 puis 3/ 8 et pas 3/10
mais heureusement que l'on trouve pareil qu'en combinatoire
(et plus rapidement)
5/10 x 4/ 9 x 3/ 8
donc pour B1,B2, D
c'est 2/3 x 1/2 = 1/3 idem combinatoire
alors que notre ami faisait
2/3 x 1/3
en ne changeant pas le dénominateur!
c'est juste qu' après le bon 5/10 ben c'est le 4/9 et pas 4/10 puis 3/ 8 et pas 3/10
mais heureusement que l'on trouve pareil qu'en combinatoire
(et plus rapidement)
5/10 x 4/ 9 x 3/ 8
donc pour B1,B2, D
c'est 2/3 x 1/2 = 1/3 idem combinatoire
alors que notre ami faisait
2/3 x 1/3
en ne changeant pas le dénominateur!
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: probabilité
Bonjour
@Beagle tu as raison. Vu que c'était faux je n'ai pas du tout compris si il y avait un raisonnement derrière cela.
A la limite ça pourrait être plus simple ayabaklouti; sauf que si on demande la probabilité d'avoir 1 bonne pièce et 2 défectueuses alors ça va se compliquer sérieusement.
@Beagle tu as raison. Vu que c'était faux je n'ai pas du tout compris si il y avait un raisonnement derrière cela.
A la limite ça pourrait être plus simple ayabaklouti; sauf que si on demande la probabilité d'avoir 1 bonne pièce et 2 défectueuses alors ça va se compliquer sérieusement.
Re: probabilité
aviateur a écrit:Bonjour
@Beagle tu as raison. Vu que c'était faux je n'ai pas du tout compris si il y avait un raisonnement derrière cela.
A la limite ça pourrait être plus simple ayabaklouti; sauf que si on demande la probabilité d'avoir 1 bonne pièce et 2 défectueuses alors ça va se compliquer sérieusement.
Salut aviateur,
Comme je suis un très mauvais calculateur, et comme en plus je suis quelqu'un peu sur de lui,
j'ai pris depuis que je suis sur maths forum l'habitude de faire le combinatoire et "l'arbre".Et j'aime bien trouver le même résultat.Dans le cas présent j'ai vainement cherché pourquoi le 10/120 ne trouvait pas pareil que le 60/1000, cela m'a troublé un moment!!!!J'étais là, mais c'est pas possible et pourquoi quoi.
C'est parfois plus difficile de détecter une faute en relisant que de refaire le machin.
Bon sinon dans le cas que tu as évoqué 1 bonne et 2 défectueuses, ben l'arbre devient un excellent apprentissage de la loi binomiale, non? une proba de base fois le nombre de branches qui realisent cette proba.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: probabilité
salut beagle, oui enfin plutôt sur le meme principe que la loi binomiale,
parce que là ce serait pas la loi binomiale, essaye pas de nous embourber dans de l'erreur,
maisoui,
une proba de base toujours la même
fois les combinaisons de branches qui amènent cette proba de base
parce que là ce serait pas la loi binomiale, essaye pas de nous embourber dans de l'erreur,
maisoui,
une proba de base toujours la même
fois les combinaisons de branches qui amènent cette proba de base
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: probabilité
beagle a écrit:Bon sinon dans le cas que tu as évoqué 1 bonne et 2 défectueuses, ben l'arbre devient un excellent apprentissage de la loi binomiale, non? une proba de base fois le nombre de branches qui réalisent cette proba.
Alors sur ce terrain des arbres je ne m'y suis jamais engagé. Donc je préfère ne rien dire.
D'abord je n'ai jamais cherché à comprendre ce genre de truc et je m'en passe très bien.
Surtout que par moment il faut plutôt une forêt qu'un arbre.
Mais attention ici, il n'y a pas de loi binomiale dans l'exercice.!!!!
Non, pour moi le meilleur apprentissage c'est de faire des choses que l'on comprend et puis c'est tout.
Bien sûr si on a le sens des probabilités, on peut faire de petits calculs comme ça mais ce qui est important c'est d'utiliser le formalisme de la proba.
Par exemple ici l'espace fondamental c'est
L' événement A dont on cherche la proba c'est le sous ensemble de
La loi est uniforme sur
C'est comme ça que je vois l'exercice. L'arbre je ne sais pas ce qu'il montre.
Pour faire l'exercice demandé c'est absolument la même chose.
Bien sûr ça fait aussi p(A)=5/10*4/9*3/8 mais comment interpréter cela en disant
je tire une pièce non défectueuse proba =5/10 puis je tire une pièce non défectueuse sachant que j'ai tiré une bonne pièce défectueuse avant proba = 4/9 puis je multiplie car les 2 en disant qu'il y a une sorte "d'indépendance". Je sais pas mais pour moi c'est pas clair.
En particulier je change un peu l'exercice: on tire 4 pièces et on calcule la proba d'avoir 1 pièce défectueuse.
Et bien je ne complique pas du tout l'exercice si on fait comme j'ai dit, il suffit de savoir compter les cardinaux. . Donc l'arbre n'est pas une bonne méthode d'apprentissage.
Re: probabilité
"
Donc l'arbre n'est pas une bonne méthode d'apprentissage."
ça c'est fort de café.
L'arbre comme recette à tout faire est à bannir en tant que recettes.
Mais l'arbre est un support d'abstraction exceptionnel en proba.
C'est comme les ensembles, c'est bien le support à l'abstraction qui fait son succès, au moins à fable niveau maths.
je serais absent demain et je dois partir, on rediscutera de cela autre jour.
Pour l'arbre de 5/10 puis 4/9
c'est un regroupent de branches toutes les branches défectueuses sont à 1/10 et ensuite tu dois bien prendre ce qui reste,
juste on regroupe les 5 branches de 1/10 en une grosse branche 5/10 ...
Donc l'arbre n'est pas une bonne méthode d'apprentissage."
ça c'est fort de café.
L'arbre comme recette à tout faire est à bannir en tant que recettes.
Mais l'arbre est un support d'abstraction exceptionnel en proba.
C'est comme les ensembles, c'est bien le support à l'abstraction qui fait son succès, au moins à fable niveau maths.
je serais absent demain et je dois partir, on rediscutera de cela autre jour.
Pour l'arbre de 5/10 puis 4/9
c'est un regroupent de branches toutes les branches défectueuses sont à 1/10 et ensuite tu dois bien prendre ce qui reste,
juste on regroupe les 5 branches de 1/10 en une grosse branche 5/10 ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: probabilité
……………………………………...
Modifié en dernier par beagle le 12 Sep 2018, 09:07, modifié 1 fois.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: probabilité
salut aviateur, tu terminais par un:
"Donc l'arbre n'est pas une bonne méthode d'apprentissage."
Donc soit c'est une parole un peu rapide, et je reste juste à discuter sur ce fil.
Soit c'est une opinion qui peut-être développée et alors je crée un fil dédié au salon pour discuter,
mais juste pour argumenter puisque c'est une ouverture pour laquelle je joue les blancs ou les noirs.
Juste pour discuter, il n' ya pas de soucis...
"Donc l'arbre n'est pas une bonne méthode d'apprentissage."
Donc soit c'est une parole un peu rapide, et je reste juste à discuter sur ce fil.
Soit c'est une opinion qui peut-être développée et alors je crée un fil dédié au salon pour discuter,
mais juste pour argumenter puisque c'est une ouverture pour laquelle je joue les blancs ou les noirs.
Juste pour discuter, il n' ya pas de soucis...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: probabilité
Juste un mot, au cas où une autre discutions ne s'ouvre pas, pour dire que sur le principe, je suis plutôt d'accord avec aviateur.
Bien évidement, et je pense que tout le monde est d'accord là dessus, les arbres en proba (comme à peu prés tout), ce n'est ni "la panacée", ni "totalement inutile" : c'est uniquement un des moyens de visualiser ce qu'il se passe dans certains contextes et la question à se poser c'est uniquement de savoir si c'est "souvent utile" ou "pas super souvent".
Et là où je pense que je rejoint aviateur, c'est qu'à mon sens, les cas où l'arbre est un support visuel vraiment meilleur que les autres, à mon sens il y en a très peu et, à mon avis, dans l'enseignement on devrait bien plus mettre l'accent sur les calculs liés au dénombrement (cas favorables / cas total) et, au niveau visuel, sur les patatoïdes.
Et face à ta question "l'arbre devient un excellent apprentissage de la loi binomiale, non ?", là, je répondrait sans la moindre ambiguïté que NON : ça n'a pas le moindre intérêt dans ce contexte là.
Si tu fait l'arbre d'une binomiale, non seulement c'est archi long, mais en plus la seule chose qui va être visuelle dessus, c'est qu'il y a 2^n issues possibles. Et par contre, LE truc important, à savoir qu'il y a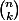 (coeff. binomial) issues où il y a k succès, là, par contre je vois vraiment pas comment tu peut le "voir" sur un arbre. Bref, ça me semble évident que tout est nettement plus visuel sur le triangle de Pascal qui lui ne fait que compter le nombre d'issues favorables sans 'intéresser au comment on en est arrivé à ces issues là.
(coeff. binomial) issues où il y a k succès, là, par contre je vois vraiment pas comment tu peut le "voir" sur un arbre. Bref, ça me semble évident que tout est nettement plus visuel sur le triangle de Pascal qui lui ne fait que compter le nombre d'issues favorables sans 'intéresser au comment on en est arrivé à ces issues là.
P.S. : de plus, il me semble qu'on en a déjà parlé dans un post. du Forum de l'intérêt (ou du non intérêt...) de présenter les proba avec des arbres.
Bien évidement, et je pense que tout le monde est d'accord là dessus, les arbres en proba (comme à peu prés tout), ce n'est ni "la panacée", ni "totalement inutile" : c'est uniquement un des moyens de visualiser ce qu'il se passe dans certains contextes et la question à se poser c'est uniquement de savoir si c'est "souvent utile" ou "pas super souvent".
Et là où je pense que je rejoint aviateur, c'est qu'à mon sens, les cas où l'arbre est un support visuel vraiment meilleur que les autres, à mon sens il y en a très peu et, à mon avis, dans l'enseignement on devrait bien plus mettre l'accent sur les calculs liés au dénombrement (cas favorables / cas total) et, au niveau visuel, sur les patatoïdes.
Et face à ta question "l'arbre devient un excellent apprentissage de la loi binomiale, non ?", là, je répondrait sans la moindre ambiguïté que NON : ça n'a pas le moindre intérêt dans ce contexte là.
Si tu fait l'arbre d'une binomiale, non seulement c'est archi long, mais en plus la seule chose qui va être visuelle dessus, c'est qu'il y a 2^n issues possibles. Et par contre, LE truc important, à savoir qu'il y a
P.S. : de plus, il me semble qu'on en a déjà parlé dans un post. du Forum de l'intérêt (ou du non intérêt...) de présenter les proba avec des arbres.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: probabilité
Voilà une position déjà plus acceptable par moi, je reprendrai ce texte si on développe.
Mais je l'ai dis je joue les blancs et les noirs dans cette affaire, donc si vous prenez les blancs, j'analyse coté noir.
Et question provoc, il ne faut pas le prendre autrement sur ce fil de discussion, POUR COMMENCER,
pour moi c'est du fun, mais allons -y, je commence par me faire plaisir.
Il ya quelques années , cela doit dater je pense maintenant, une question de proba au bac, il s'agit , classique, de boules, et c'est prendre 3 boules dans un sac de boules.
La réponse attendue est une démonstration avec des combinaisons , avec du C, vu que choisir 3 dans n , ben déjà en le disant, on sait à quel chapitre on est.
Sauf que cela se fait très bien également, par tirages successifs, et bing et bang du 5/8 premiere boule fois 2/7 la deuxième fois 4/6 la troisième.Un truc qui donne le résultat rapidement et qui est tout aussi facile à appréhender que le C(n,k).
Bref la plupart des académies donnent les points à la question, d'autres académies donnent zéro, avec pour raison que l'on utilise du tirage successif pour se ramener à un tirage en une fois de 3 boules.
Alors vous m'avez vu arriver avec mes gros sabots,
nous avons ici un exo de tirage successifs sans remise et vous démarrez une démonstration à base de C,
et moi dont la mauvaise foi est en jeu, je dis, ben non je ne comprends pas qu'un tirage successif cela soit la même chose que prendre et calculer du C qui choisit 3 en groupe et non pas un par un.
Sans parler de l'ordre, ètes vous sur que l'on doit utiliser du C et pas du A,
Bref, je sais pas si je dois vous donner les points , moi...
Mais je l'ai dis je joue les blancs et les noirs dans cette affaire, donc si vous prenez les blancs, j'analyse coté noir.
Et question provoc, il ne faut pas le prendre autrement sur ce fil de discussion, POUR COMMENCER,
pour moi c'est du fun, mais allons -y, je commence par me faire plaisir.
Il ya quelques années , cela doit dater je pense maintenant, une question de proba au bac, il s'agit , classique, de boules, et c'est prendre 3 boules dans un sac de boules.
La réponse attendue est une démonstration avec des combinaisons , avec du C, vu que choisir 3 dans n , ben déjà en le disant, on sait à quel chapitre on est.
Sauf que cela se fait très bien également, par tirages successifs, et bing et bang du 5/8 premiere boule fois 2/7 la deuxième fois 4/6 la troisième.Un truc qui donne le résultat rapidement et qui est tout aussi facile à appréhender que le C(n,k).
Bref la plupart des académies donnent les points à la question, d'autres académies donnent zéro, avec pour raison que l'on utilise du tirage successif pour se ramener à un tirage en une fois de 3 boules.
Alors vous m'avez vu arriver avec mes gros sabots,
nous avons ici un exo de tirage successifs sans remise et vous démarrez une démonstration à base de C,
et moi dont la mauvaise foi est en jeu, je dis, ben non je ne comprends pas qu'un tirage successif cela soit la même chose que prendre et calculer du C qui choisit 3 en groupe et non pas un par un.
Sans parler de l'ordre, ètes vous sur que l'on doit utiliser du C et pas du A,
Bref, je sais pas si je dois vous donner les points , moi...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: probabilité
Pour moi, ce type de truc sur un sujet du bac, c'est caricatural de ce que j'aurais tendance à appeler de "l'enculage de mouche" et qui, hélas, a de plus en plus tendance à remplacer un réel débat concernant les objectifs (à court et long termes) des programmes des collèges Lycée.
Quand tu donne un exo. de math, si tu ne spécifie pas explicitement que tu veut que telle ou telle méthode particulière soit employée (*), alors la seule chose que tu as à noter, c'est la cohérence du raisonnement et la justesse des calculs. Si c'est O.K. (pour les deux), ben tu met la note max et c'est tout.
Si le type à employé une méthode pourrie, ben il s'est auto sanctionné vu qu'il a perdu du temps sur la question et je vois pas l'intérêt de le re-sanctionner une deuxième fois sur la note.
Si le type au contraire a gagné du temps en trouvant une méthode plus maline que celle à laquelle tu pensait, ben c'est qu'il est plus malin que toi, et je vois pas vraiment de quel droit tu pourrait te permettre de le sanctionner (je rappelle bien évidement que tout ça, c'est modulo que le raisonnement soit correct)
Le seul cas un peu délicat que j'ai (rarement) vu, c'est celui qui va beaucoup plus vite que prévu, mais en utilisant des outils qui ne sont pas au programme comme par exemple de montrer qu'une matrice est inversible avec les déterminant alors que les déterminants n'ont pas encore été vu en cours (mais lui les connaît soit du fait d'un parcours atypique, soit parce qu'il les a étudié tout seul).
(*) Et quand je le fait, systématiquement je souligne le morceau de phrase en utilisant la méthode tartenpion
Quand tu donne un exo. de math, si tu ne spécifie pas explicitement que tu veut que telle ou telle méthode particulière soit employée (*), alors la seule chose que tu as à noter, c'est la cohérence du raisonnement et la justesse des calculs. Si c'est O.K. (pour les deux), ben tu met la note max et c'est tout.
Si le type à employé une méthode pourrie, ben il s'est auto sanctionné vu qu'il a perdu du temps sur la question et je vois pas l'intérêt de le re-sanctionner une deuxième fois sur la note.
Si le type au contraire a gagné du temps en trouvant une méthode plus maline que celle à laquelle tu pensait, ben c'est qu'il est plus malin que toi, et je vois pas vraiment de quel droit tu pourrait te permettre de le sanctionner (je rappelle bien évidement que tout ça, c'est modulo que le raisonnement soit correct)
Le seul cas un peu délicat que j'ai (rarement) vu, c'est celui qui va beaucoup plus vite que prévu, mais en utilisant des outils qui ne sont pas au programme comme par exemple de montrer qu'une matrice est inversible avec les déterminant alors que les déterminants n'ont pas encore été vu en cours (mais lui les connaît soit du fait d'un parcours atypique, soit parce qu'il les a étudié tout seul).
(*) Et quand je le fait, systématiquement je souligne le morceau de phrase en utilisant la méthode tartenpion
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: probabilité
Salut Ben314,
je ne peux que louer ta grande sagesse habituelle.
Il me semble que soit c'est dit dans l'énoncé, soit cela doit ètre au mieux conçu dans l'exo pour etre plus ch.ant autrement.
Sinon pour l'arbre, au-delà de l'entame sus-jaccente j'ai relancé car en effet tu avais déjà dit ètre gonflé par l'arbre, mais alors tu avais développé surtout le caractère c'est des probas, je fais mon arbre qui était pénible en tant que recette,
aviateur revenant à la charge en disant que c'est pas bon pédagogiquement, alors là je pense que l'on peut discuter … pas pour troller et faire des pages, mais discuter je pense que l'on peut utiliser de tels trucs pour dire, c'est quoi les maths, et aviateur nous parle du formalisme à respecter, et c'est quoi enseigner les maths, c'est quoi recevoir les maths, c'est quoi construire les maths, parce que cela me semble assez différent, et je veux bien dire ce que j'avais en tète sur l'arbre ...
je ne peux que louer ta grande sagesse habituelle.
Il me semble que soit c'est dit dans l'énoncé, soit cela doit ètre au mieux conçu dans l'exo pour etre plus ch.ant autrement.
Sinon pour l'arbre, au-delà de l'entame sus-jaccente j'ai relancé car en effet tu avais déjà dit ètre gonflé par l'arbre, mais alors tu avais développé surtout le caractère c'est des probas, je fais mon arbre qui était pénible en tant que recette,
aviateur revenant à la charge en disant que c'est pas bon pédagogiquement, alors là je pense que l'on peut discuter … pas pour troller et faire des pages, mais discuter je pense que l'on peut utiliser de tels trucs pour dire, c'est quoi les maths, et aviateur nous parle du formalisme à respecter, et c'est quoi enseigner les maths, c'est quoi recevoir les maths, c'est quoi construire les maths, parce que cela me semble assez différent, et je veux bien dire ce que j'avais en tète sur l'arbre ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Re: probabilité
Salut aviateur, juste un petit mot sur ta phrase.
Sans polémique inutile, cela servira juste à éventuellement discuter pédagogie, apprentissage.
Sans polémique inutile, cela servira juste à éventuellement discuter pédagogie, apprentissage.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
39 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
