Espace affine

[coc0]

Bonjour,

J'aurai une question concernant cette phrase:
Pour , on note sous la forme

Je ne comprends pas pourquoi on introduit la notation enfaite. Pourriez vous parler de cette expression?

Merci d'avance pour votre aide et votre attention

[Ben314]

Salut.
Je comprend pas de quelle notation tu parle.
Pour qu'un ensemble soit un espace affine sur l'espace vectoriel , il faut, par définition (c.f. par exemple Wiki)
qu'il y ait une application telle que :



Ensuite, pour tout et tout , le (1) dit qu'il existe un unique tel que et ce point est noté .

Le seul truc qui me vient à l'esprit concernant une notation où le apparaîtrait avant le , c'est celle correspondant à la notion de translation : pour fixé, l'application qui à associe ce fameux (unique) tel que est appelée "translation de vecteur " et est souvent noté (où =lettre grecque tau=t comme translation) ce qui permet d'écrire (avec les deux notations) que

[coc0]

Bonjour Ben314,

Merci pour votre réponse.
Vous avez plutôt bien éclairé ma lanterne sur certain point.

Dans mon livre, ils introduisent un espace affine comme étant un ensemble muni d'une action libre et transitive du groupe additif sous-jacent à un espace vectoriel .

Puis ils définissent une action,
une action: cela signifie que l'on a un morphisme de groupe de vers le groupe des permutations de et qui à un vecteur associe la permutation

Puis, ils définissent:
Pour , on note sous la forme


pour dire que comme est un morphisme de groupe, on a



Ainsi, c'est la notation de type et que je ne comprends pas vraiment. Pensez vous que cela est en lien avec le "tau" dont vous parlez?

PS: désolé si mes questions paraissent bêtes, cette définition englobe beaucoup de nouvelles notions pour moi.

Merci beaucoup

[Ben314]

Ben oui, c'est très exactement la même chose énoncé avec un vocabulaire légèrement plus technique :
- Au lieu de parler comme dans le (1) de mon post de "bijections", ton truc parle à la place de "permutation", mais j'espère que tu sait que c'est la même chose.
- La fameuse "permutation associée au vecteur ", bon, ben là y'a pas photo, tout le monde apelle ça la "translation de vecteur " (et je comprend toujours pas où tu as bien pu pécher ta notation : un truc style avec un T comme translation, j'aurais sans doute compris, mais le fait d'utiliser l'ensemble vide comme symbole fonctionnel, ça je crois que je l'ai jamais vu).
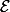
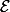
- Et effectivement, la relation de Chasles (i.e. la condition (2) de la définition de mon post précédent), si on veut, on peut l'écrire sous la forme (*) ce qui signifie très précisément que l'application du groupe dans le groupe des bijections de dans muni de la loi de composition est un morphisme de groupe. Et ça, ben c'est justement la définition d'un "groupe opérant sur un ensemble".

(*) L'équivalence entre les deux formulations de la relation de Chasles est un mini exo. de "logique pure" que je t'incite fortement à faire.