Sous-groupe engendré par une partie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Lorem
- Messages: 4
- Enregistré le: 03 Sep 2018, 19:05
-
 par Lorem » 03 Sep 2018, 19:10
par Lorem » 03 Sep 2018, 19:10
Bonjour,
Je souhaiterais démontrer la proposition suivante.
Soit
)
un groupe et

une partie de

. On note

l'ensemble des mots s'écrivant avec des éléments (et/ou des inverses d'éléments) de

. Alors on a
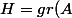)
.
J'ai déjà prouvé que

est un sous-groupe de

et

est trivial.
Je ne sais pas comment obtenir le résultat: Si
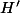
est un sous-groupe de

contenant

alors

.
Merci d'avance

-
aviateur
 par aviateur » 03 Sep 2018, 19:41
par aviateur » 03 Sep 2018, 19:41
Si
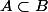
prouve que
\subset gr(B))
et c'est gagné.
-
Lorem
- Messages: 4
- Enregistré le: 03 Sep 2018, 19:05
-
 par Lorem » 03 Sep 2018, 19:45
par Lorem » 03 Sep 2018, 19:45
Quel est l'ensemble

? Je n'avais envisagé qu'une partie:

-
aviateur
 par aviateur » 03 Sep 2018, 19:51
par aviateur » 03 Sep 2018, 19:51
B c'est n'importe quoi (ds G bien sûr), au départ pas forcément un groupe.
-
Lorem
- Messages: 4
- Enregistré le: 03 Sep 2018, 19:05
-
 par Lorem » 03 Sep 2018, 20:00
par Lorem » 03 Sep 2018, 20:00
Je vais essayer ça merci

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Sep 2018, 20:38
par Ben314 » 03 Sep 2018, 20:38
Salut,
J'ai pas bien compris l'indic. d'aviateur : ce qu'il demande de montrer est certes vrai, mais je vois pas bien le rapport avec la question posée.
Et sinon, perso, ce que j'aurais donné comme "indic", c'est :
- C'est quoi la définition d'un sous groupe ?
- Si on écrit un "mot" avec des élément (ou leur inverse) qui sont tous dans un certain sous groupe H, que peut on dire du résultat ?
EDIT : En réfléchissant un peu plus (comme quoi ça sert des fois...) je pense avoir compris l'indic d'aviateur : il veut ensuite utiliser la propriété dont il parle au cas où B=H après avoir remarqué que, si H est un sous groupe, alors gr(H)=H.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 03 Sep 2018, 20:41
par aviateur » 03 Sep 2018, 20:41
Salut, on est pas sur la même longueur d'onde ou quoi?
si B=H' en particulier gr(H')=H' et c'est tout.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Sep 2018, 20:42
par Ben314 » 03 Sep 2018, 20:42
Oui, je viens de voir.
Désolé.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
aviateur
 par aviateur » 03 Sep 2018, 20:44
par aviateur » 03 Sep 2018, 20:44
c'est pas grave ça arrive même au gens bien.
D'ailleurs ici je regarde un film comique et je peux me planter à coup sûr.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Sep 2018, 20:56
par Ben314 » 03 Sep 2018, 20:56
Moi je me refait pour la 10em fois les Dr House en streaming...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Lorem
- Messages: 4
- Enregistré le: 03 Sep 2018, 19:05
-
 par Lorem » 08 Sep 2018, 08:41
par Lorem » 08 Sep 2018, 08:41
J'ai finalement réussi la démonstration merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités