Solution tricolore...
14 messages
- Page 1 sur 1
Solution tricolore...
Salut,
On "colorie" les entiers de 1 à 2018 en Bleu, Blanc, Rouge (un entier = une couleur) de façon à ce qu'il y en ait au moins 505 de chaque couleur.
Montrer qu'il existe au moins une solution tricolore à l'équation X+Y=Z.
(tiré du même bouquin que la précédente)
On "colorie" les entiers de 1 à 2018 en Bleu, Blanc, Rouge (un entier = une couleur) de façon à ce qu'il y en ait au moins 505 de chaque couleur.
Montrer qu'il existe au moins une solution tricolore à l'équation X+Y=Z.
(tiré du même bouquin que la précédente)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Solution tricolore...
Salut,
Une solution possible est de transformer en deux couleurs : A et B et de colorier les entiers de 7 à 2018 avec la séquence ABBA (possible car 2018-7+1 = 2012, un multiple de 4), on obtient 1006 entiers de chaque couleur.
On prend la séquence 1,2, ... 6 et on forme on colorie 1,2,3 et 5 en A et 4,6 en B.
On a maintenant 1010 entiers en couleur A, que on peut diviser en deux ensembles de cardinal égal (505 éléments) de la façon qu'on veut pour former X et Y. Z est l'ensemble de couleur B qui contient 1008 éléments.
Une solution possible est de transformer en deux couleurs : A et B et de colorier les entiers de 7 à 2018 avec la séquence ABBA (possible car 2018-7+1 = 2012, un multiple de 4), on obtient 1006 entiers de chaque couleur.
On prend la séquence 1,2, ... 6 et on forme on colorie 1,2,3 et 5 en A et 4,6 en B.
On a maintenant 1010 entiers en couleur A, que on peut diviser en deux ensembles de cardinal égal (505 éléments) de la façon qu'on veut pour former X et Y. Z est l'ensemble de couleur B qui contient 1008 éléments.
Re: Solution tricolore...
Je comprend pas bien ce que tu cherche à faire, ni le lien avec l'énoncé...
Comme c'est éventuellement qu'il n'est pas clair, je vais le réécrire de façon plus mathématique :
Montrer que, quelque soit la fonction vérifiant
vérifiant \big)\!\geq\!505) , il existe forcément
, il existe forcément  (dépendant bien sûr de
(dépendant bien sûr de  ) tels que
) tels que  et
et \!=\!\{\text{Bleu},\text{Blanc},\text{Rouge}\}) .
.
Comme c'est éventuellement qu'il n'est pas clair, je vais le réécrire de façon plus mathématique :
Montrer que, quelque soit la fonction
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Solution tricolore...
Ah merci, c'est plus clair  J'avais compris qu'il fallait colorier les entiers en trois couleur de manière à ce que la somme des éléments de deux couleurs soit égale à la somme des éléments de la dernière couleur
J'avais compris qu'il fallait colorier les entiers en trois couleur de manière à ce que la somme des éléments de deux couleurs soit égale à la somme des éléments de la dernière couleur
Re: Solution tricolore...
Transformons l'équation en X = Z - Y et trouvons quel X va "déranger" : 4
Une fois les entiers coloriés, le nombre 4 doit bien être d'une couleur appelons la : A et les deux autres B et C.
Le but étant de trouver un entier en B et un autre en C dont la différence fait 4, dans le pire des cas les élément colorié en B et en C sont minimum donc a 505 entiers chacun, il reste 1007 entiers en A (sans compter 4).
Si le coloriage s'est effectué sur 503 entiers de B, 503 entiers de C et 1006 entiers de A consécutifs, en un telle séquence :
ABCAACBA, BACAACB ou un cycle d'un de ces derniers (on glisse les lettre d'un côté en on les remets de l'autre) :
On sait qu'il reste des entier; 2 en B, 2 en C et 1 en A, ils sont placé au début et/ou à la fin des séquences, regardons les premiers entiers :
1 2 3 4 5 6, 4 est de couleur A, soit on ne peut pas colorier de façon ne pas faire une différence de 4 entre un entiers en B et un en C, soit nous avons quelque chose de la sorte:
ACBACB, et on remarque une solution tricolore (ici 1 + 2 = 3)
Une fois les entiers coloriés, le nombre 4 doit bien être d'une couleur appelons la : A et les deux autres B et C.
Le but étant de trouver un entier en B et un autre en C dont la différence fait 4, dans le pire des cas les élément colorié en B et en C sont minimum donc a 505 entiers chacun, il reste 1007 entiers en A (sans compter 4).
Si le coloriage s'est effectué sur 503 entiers de B, 503 entiers de C et 1006 entiers de A consécutifs, en un telle séquence :
ABCAACBA, BACAACB ou un cycle d'un de ces derniers (on glisse les lettre d'un côté en on les remets de l'autre) :
On sait qu'il reste des entier; 2 en B, 2 en C et 1 en A, ils sont placé au début et/ou à la fin des séquences, regardons les premiers entiers :
1 2 3 4 5 6, 4 est de couleur A, soit on ne peut pas colorier de façon ne pas faire une différence de 4 entre un entiers en B et un en C, soit nous avons quelque chose de la sorte:
ACBACB, et on remarque une solution tricolore (ici 1 + 2 = 3)
Re: Solution tricolore...
Bonjour
il me semble que j'ai la démo après avoir ramer mais c'est un peu long.
J'envoie le début mais je finirai plus tard. .
Je désigne par R la couleur rouge, B la couleur bleu et W la couleur blanche (white)
Soit E=[[1,2018]] et u l'application de E dans {R,B,W} qui désigne la couleur d'un nombre de E.
Sans restreindre la généralité quand je parcours E ds l'ordre croissant je rencontre les couleurs ds cet ordre: R , B, W.
C'est à dire que u(1)=R et avec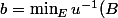, w=\min_E u^{-1}(W)) on a
on a
 et
et =R, \forall j=1,...,b-1.)
Je suppose qu'il n'existe pas de triplet X+Y=Z tels que u(X),u(Y),u(z} soient trois couleurs différentes.
remarque pour tout z tel que z=x+y , l'égalité u(z)=u(x)+u(y) signifiera (d'après l'hypothèse) que u(z)=u(x) ou bien u(y).
Quelques lemmes
lemme 1: pour tout=R.)
preuve: en effet, w=j+(w-j) donc u(w)=u(j)+u(w-j)=W=R+u(w-j).
Mais comme\neq W) alors
alors =R) . fin preuve
. fin preuve
lemme 2: u(w-b)=B.
preuve: en effet, w=b+(w-b) donc u(w)=u(b)+u(w-b)=W=B+u(w-j).
Mais comme\neq W) alors u(w-b)=B. fin preuve
alors u(w-b)=B. fin preuve
remarque: le cas w-b=b n'est pas exclus.
Posons maintenant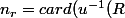), n_b=card (u^{-1}(B)),n_w=card (u^{-1}(W)).)
Evidemment on a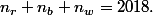 Et rappelons que
Et rappelons que
Notons aussi:
=\lbrace {w_1,w_2,...,w_{n_w} \rbrace)
Avec les notations précédentes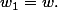
lemme 3. u(w+k)(=u(w_1)+k)=R, k=1,...,b-1
preuve: u(w+k)=u(w)+u(k)=W+R. Mais aussi u(w+k)=u(b+(w-(b-k))=u(b)+u(w-(b-k))=B++u(w-(b-k))
mais b-k<b dc (cf lemme 1) u(w-(b-k))=R.
On a donc u(w+k)=B+R=W+R i.e u(w+k)=R. fin preuve.
il me semble que j'ai la démo après avoir ramer mais c'est un peu long.
J'envoie le début mais je finirai plus tard. .
Je désigne par R la couleur rouge, B la couleur bleu et W la couleur blanche (white)
Soit E=[[1,2018]] et u l'application de E dans {R,B,W} qui désigne la couleur d'un nombre de E.
Sans restreindre la généralité quand je parcours E ds l'ordre croissant je rencontre les couleurs ds cet ordre: R , B, W.
C'est à dire que u(1)=R et avec
Je suppose qu'il n'existe pas de triplet X+Y=Z tels que u(X),u(Y),u(z} soient trois couleurs différentes.
remarque pour tout z tel que z=x+y , l'égalité u(z)=u(x)+u(y) signifiera (d'après l'hypothèse) que u(z)=u(x) ou bien u(y).
Quelques lemmes
lemme 1: pour tout
preuve: en effet, w=j+(w-j) donc u(w)=u(j)+u(w-j)=W=R+u(w-j).
Mais comme
lemme 2: u(w-b)=B.
preuve: en effet, w=b+(w-b) donc u(w)=u(b)+u(w-b)=W=B+u(w-j).
Mais comme
remarque: le cas w-b=b n'est pas exclus.
Posons maintenant
Evidemment on a
Notons aussi:
Avec les notations précédentes
lemme 3. u(w+k)(=u(w_1)+k)=R, k=1,...,b-1
preuve: u(w+k)=u(w)+u(k)=W+R. Mais aussi u(w+k)=u(b+(w-(b-k))=u(b)+u(w-(b-k))=B++u(w-(b-k))
mais b-k<b dc (cf lemme 1) u(w-(b-k))=R.
On a donc u(w+k)=B+R=W+R i.e u(w+k)=R. fin preuve.
Re: Solution tricolore...
lemme 4. =R, \forall k=1,...,b-1)
preuve=u(w_2-k+k)=u(w_2-k)+u(k)=u(w_2-k) + R)
mais (conséquence directe du lemme précédent)donc
(conséquence directe du lemme précédent)donc \neq W)
Il vient dc u(w_2-k)=R. fin preuve.
remarque les cas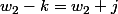 pour j,k dans [[1,b-1] n'est pas exclus.
pour j,k dans [[1,b-1] n'est pas exclus.
lemme 5. (Généralisation des lemme 3 et 4. )
=R) (excepté les cas
(excepté les cas ) .
.
preuve reprendre les démonstrations des lemmes 3 et 4.
fin preuve.
lemme 6. b=2.
preuve Les lemmes précédents montrent que pour il y a au moins
il y a au moins
2(b-1) nombres qui ont une couleur rouge et entre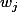 et
et  il y a au moins
il y a au moins
(b-1) couleurs rouge.
On a donc+(n_w-1)(b-1)=(b-1)(n_w+1)\geq (b-1) 506)
Il vient donc 506 + 505+505.)
Ce qui donne et donc b=2. fin preuve.
et donc b=2. fin preuve.
preuve
mais
Il vient dc u(w_2-k)=R. fin preuve.
remarque les cas
lemme 5. (Généralisation des lemme 3 et 4. )
preuve reprendre les démonstrations des lemmes 3 et 4.
fin preuve.
lemme 6. b=2.
preuve Les lemmes précédents montrent que pour
2(b-1) nombres qui ont une couleur rouge et entre
(b-1) couleurs rouge.
On a donc
Il vient donc
Ce qui donne
Re: Solution tricolore...
C'est vrai que perso, je n'ai pas compris non plus la preuve de FLBP, quoique je pense qu'il a mis le doigt au bon endroit, j'ai tout de même compris son histoire de " 4 ".
Je développe :
Désignons A la 1ère couleur placée dans l'ordre (donc en 1), B la seconde et C la 3ème.
Si C est en k, alors les couples :
(1 , k-1) (2, k-2) (3,k-3)....sont forcément constitués de 2 éléments d'une même couleur. Il y a symétrie d'axe C/2.
Ensuite, en k+1, on est obligé de placer A puisque (1,k) =A C et que, du fait de la symétrie perdue, il existe (n,k+1-n) = AB ou BA.
De proche en proche, on se rend compte qu'on est obligé de reproduire la séquence de 1 à k-1. C'est seulement en 2k, car à nouveau on retrouve de la symétrie, qu'on peut placer ce qu'on veut, mais alors on a intérêt à mettre C car c'est le seul endroit où on peut le placer, et il faudra bien en mettre 505.
On est donc obligé, du fait de la contrainte de placement de C, d'avoir une séquence la plus courte possible:
ABA, et c'est seulement en position 4 qu'on peut placer C.
Maintenant, si on compte bien, on ne peut placer que 504 C, ou bien 505 C mais seulement 504 B, A ayant 1009 éléments.
CQFD
Je développe :
Désignons A la 1ère couleur placée dans l'ordre (donc en 1), B la seconde et C la 3ème.
Si C est en k, alors les couples :
(1 , k-1) (2, k-2) (3,k-3)....sont forcément constitués de 2 éléments d'une même couleur. Il y a symétrie d'axe C/2.
Ensuite, en k+1, on est obligé de placer A puisque (1,k) =A C et que, du fait de la symétrie perdue, il existe (n,k+1-n) = AB ou BA.
De proche en proche, on se rend compte qu'on est obligé de reproduire la séquence de 1 à k-1. C'est seulement en 2k, car à nouveau on retrouve de la symétrie, qu'on peut placer ce qu'on veut, mais alors on a intérêt à mettre C car c'est le seul endroit où on peut le placer, et il faudra bien en mettre 505.
On est donc obligé, du fait de la contrainte de placement de C, d'avoir une séquence la plus courte possible:
ABA, et c'est seulement en position 4 qu'on peut placer C.
Maintenant, si on compte bien, on ne peut placer que 504 C, ou bien 505 C mais seulement 504 B, A ayant 1009 éléments.
CQFD
Re: Solution tricolore...
Bonjour @nogdim merci de ces quelques clarifications. Comme tu le dis "il a mis le doigt dessus". Mais je dirai qu'on devine que la dessous il y a quelque chose. Néanmoins une preuve c'est quelque chose que l'on essaye de rédiger de façon à être compris par les autres. Bien sûr on est sur un forum mais tout de même.
Maintenant malgré tes efforts, il y a encore des passages qui restent obscurs:
Juste avant cette phrase c'est OK mais là. on se rend compte qu'on est obligé ... Admettons mais pourquoi?
"C'est seulement en 2k car à nouveau on retrouve de la symétrie??" idem.
Maintenant malgré tes efforts, il y a encore des passages qui restent obscurs:
nodgim a écrit:De proche en proche, on se rend compte qu'on est obligé de reproduire la séquence de 1 à k-1. C'est seulement en 2k, car à nouveau on retrouve de la symétrie, qu'on peut placer ce qu'on veut, mais alors on a intérêt à mettre C car c'est le seul endroit où on peut le placer, et il faudra bien en mettre 505.
Juste avant cette phrase c'est OK mais là. on se rend compte qu'on est obligé ... Admettons mais pourquoi?
"C'est seulement en 2k car à nouveau on retrouve de la symétrie??" idem.
Re: Solution tricolore...
Bien sûr j'ai fait court,déjà tu as compris le début et l'histoire de la symétrie, car c'est là, à mon avis, le secret de l'énigme.
Sur un exemple (généralisable) :
AABBA : tant qu'on ne place que 2 couleurs, on les place comment on veut. Il faut de la symétrie pour placer C: AABBABBAAC.
Maintenant, c'est peut être le plus délicat pour placer les suivants. On regarde évidemment les couples (1,10) (2,9)....: AC empêche de placer B et comme on a perdu la symétrie, il y a forcément des couples AB, donc on ne peut que placer A : AABBABBAACA. Idem pour le suivant à cause de AC en (2,10).
AABBABBAACAA. B obligé pour le suivant à cause du couple BC en ( 3, 10) et BA en (4,9)
AABBABBAACAAB. B obligé pour le suivant à cause de BC en (4,10) et AB.
AABBABBAACAABB. A obligé pour le suivant à cause de AC en (5,10) et AB
AABBABBAACAABBA. BBAA obligés pour la suite.
AABBABBAACAABBABBAA: Symétrie d'axe C, on peut placer ce qu'on veut, mais si on ne met pas C, on est mal car il faudra retrouver de la symétrie entre les A et les B, C va être plus rare encore.
On est donc obligé de recopier la séquence où apparait le 1er C. et de proche en proche d'aller ainsi jusqu'au bout des 2018 couleurs.
Sur un exemple (généralisable) :
AABBA : tant qu'on ne place que 2 couleurs, on les place comment on veut. Il faut de la symétrie pour placer C: AABBABBAAC.
Maintenant, c'est peut être le plus délicat pour placer les suivants. On regarde évidemment les couples (1,10) (2,9)....: AC empêche de placer B et comme on a perdu la symétrie, il y a forcément des couples AB, donc on ne peut que placer A : AABBABBAACA. Idem pour le suivant à cause de AC en (2,10).
AABBABBAACAA. B obligé pour le suivant à cause du couple BC en ( 3, 10) et BA en (4,9)
AABBABBAACAAB. B obligé pour le suivant à cause de BC en (4,10) et AB.
AABBABBAACAABB. A obligé pour le suivant à cause de AC en (5,10) et AB
AABBABBAACAABBA. BBAA obligés pour la suite.
AABBABBAACAABBABBAA: Symétrie d'axe C, on peut placer ce qu'on veut, mais si on ne met pas C, on est mal car il faudra retrouver de la symétrie entre les A et les B, C va être plus rare encore.
On est donc obligé de recopier la séquence où apparait le 1er C. et de proche en proche d'aller ainsi jusqu'au bout des 2018 couleurs.
Re: Solution tricolore...
Rebonjour alors maintenant je ne comprends plus rien: et J'explique ce que je ne comprends pas.
Est ce un raisonnement par l'absurde? Cela n'a pas été dit clairement: mais cela y ressemble. Sinon les couleurs on ne les place pas où on veut. Elles sont là aléatoirement avec la seule condition c'est que chaque couleur soit représentées au moins 505 fois.
Cela ne peut être qu'un raisonnement par l'absurde.
Alors je ne sais pas si vous avez lu ma démo (le début car je n'ai pas fini):
dedans il y a
1- le fait que je raisonne par l'absurde
2- que j'utilise la symétrie (donc ça c'est sûr que ça joue un rôle et que je l'ai vu)
3- et puis il y a le lemme 6 où je suis arrivé qui dit que la seule valeur possible est b=2.
Traduit avec vos notations cela veut dire la première couleur étant A (i.e u(1)=A) alors la couleur suivante ne peut être que B (i.e u(2)=B) .
"Tant que l'on ne place que 2 couleurs on les place comme on veut AABB..? "
Et c'est ça qui me gêne par rapport à ce que je sais
C'est toujours pareil quand il y a une faille quelque part il faut la lever.
Je ne dis pas avoir raison mais je trouve des contradictions entre les 2 démonstrations. Il faut régler le problème.
Est ce un raisonnement par l'absurde? Cela n'a pas été dit clairement: mais cela y ressemble. Sinon les couleurs on ne les place pas où on veut. Elles sont là aléatoirement avec la seule condition c'est que chaque couleur soit représentées au moins 505 fois.
Cela ne peut être qu'un raisonnement par l'absurde.
Alors je ne sais pas si vous avez lu ma démo (le début car je n'ai pas fini):
dedans il y a
1- le fait que je raisonne par l'absurde
2- que j'utilise la symétrie (donc ça c'est sûr que ça joue un rôle et que je l'ai vu)
3- et puis il y a le lemme 6 où je suis arrivé qui dit que la seule valeur possible est b=2.
Traduit avec vos notations cela veut dire la première couleur étant A (i.e u(1)=A) alors la couleur suivante ne peut être que B (i.e u(2)=B) .
"Tant que l'on ne place que 2 couleurs on les place comme on veut AABB..? "
Et c'est ça qui me gêne par rapport à ce que je sais
C'est toujours pareil quand il y a une faille quelque part il faut la lever.
Je ne dis pas avoir raison mais je trouve des contradictions entre les 2 démonstrations. Il faut régler le problème.
Re: Solution tricolore...
Rebonjour Je continue ma démo.
Avant tout je fais le point de ce qui a été fait et résume des conséquences évidentes des lemmes déjà établis:
1 Raisonnement par l'absurde (c'est à dire que je suppose qu'il n'y a pas de solution se X+Y=Z avec trois couleurs différente
2. Les deux premières couleurs sont couleurs nécessairement u(1)=R et u(2)=W
3. u(3)=W n'est pas possible ( à cause des "symétries" voir lemme)
4. Pour tout k tel que u(k)=W alors u(k-1)=u(k+1)=R
Pour la suite je désigne par m et p deux couleurs W consécutives. Ce qui veut dire que
m<p , u(m)=u(p)=w et pour tout\neq w.)
Désignons par d=m-p la distance entre 2 couleurs consécutives. Nécessairement on a .
.
Les configurations possibles pour les différentes valeurs de d sont
d=2: ---- - (pourvu que
- (pourvu que  )
)
d=3: ---- ---
---
d=4 : ---- ---
---
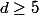 : ----
: ---- ---
---
Lemme 7 La configuration avec d=3 n'est pas possible
Preuve utiliser le lemme 6: u(2)=B
Lemme 8. u(3)=R
Preuve. supposons que cela ne soit pas le cas alors u(3)=B. Mais alor la configuration d=2 n'est pas possible.
En effet cela vient de m+2=m-1+3 donc W=u(m+2)=u(m-1)+u(3)=R+B (imp).
La conséquence est que . Entre 2 W consécutifs il y a au moins de R et 1 W.
. Entre 2 W consécutifs il y a au moins de R et 1 W.
Faisons le compte des nombres entre W_1 et W_{n_r}:
On a n_r W et au moins 2 (n_r-1) R + (n_r-1) B ,
ce qui fait au moins 4 n_r-3 nombres auquel je peux ajouter les 3 premières couleurs R,B,R non encore comptabiliser. Ce qui fait au moins 4 n_r couleurs.
Donc donne
donne  (comme par hasard!!)
(comme par hasard!!)
Contradiction
fin preuve
Avant tout je fais le point de ce qui a été fait et résume des conséquences évidentes des lemmes déjà établis:
1 Raisonnement par l'absurde (c'est à dire que je suppose qu'il n'y a pas de solution se X+Y=Z avec trois couleurs différente
2. Les deux premières couleurs sont couleurs nécessairement u(1)=R et u(2)=W
3. u(3)=W n'est pas possible ( à cause des "symétries" voir lemme)
4. Pour tout k tel que u(k)=W alors u(k-1)=u(k+1)=R
Pour la suite je désigne par m et p deux couleurs W consécutives. Ce qui veut dire que
m<p , u(m)=u(p)=w et pour tout
Désignons par d=m-p la distance entre 2 couleurs consécutives. Nécessairement on a
Les configurations possibles pour les différentes valeurs de d sont
d=2: ----
d=3: ----
d=4 : ----
Lemme 7 La configuration avec d=3 n'est pas possible
Preuve utiliser le lemme 6: u(2)=B
Lemme 8. u(3)=R
Preuve. supposons que cela ne soit pas le cas alors u(3)=B. Mais alor la configuration d=2 n'est pas possible.
En effet cela vient de m+2=m-1+3 donc W=u(m+2)=u(m-1)+u(3)=R+B (imp).
La conséquence est que
Faisons le compte des nombres entre W_1 et W_{n_r}:
On a n_r W et au moins 2 (n_r-1) R + (n_r-1) B ,
ce qui fait au moins 4 n_r-3 nombres auquel je peux ajouter les 3 premières couleurs R,B,R non encore comptabiliser. Ce qui fait au moins 4 n_r couleurs.
Donc
Contradiction
fin preuve
Re: Solution tricolore...
Aviateur,
Je n'ai pas lu en détail ce que tu as fait, mais ça me semble être la même preuve, ou à peu près, que la tienne, néanmoins tu as fait plus rigoureux et abouti, alors qu'il reste des points obscurs dans la mienne.
Sinon :
"Tant que l'on ne place que 2 couleurs on les place comme on veut AABB..? "
Et c'est ça qui me gêne par rapport à ce que je sais .
Là c'est évident, puisque la contrainte "ABC" ne commence qu'avec la 3ème couleur placée pour la 1ère fois.
Je n'ai pas lu en détail ce que tu as fait, mais ça me semble être la même preuve, ou à peu près, que la tienne, néanmoins tu as fait plus rigoureux et abouti, alors qu'il reste des points obscurs dans la mienne.
Sinon :
"Tant que l'on ne place que 2 couleurs on les place comme on veut AABB..? "
Et c'est ça qui me gêne par rapport à ce que je sais .
Là c'est évident, puisque la contrainte "ABC" ne commence qu'avec la 3ème couleur placée pour la 1ère fois.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 1 invité
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
