Equivalence d'énoncés d'algèbre linéaire ?

[M.Floquet]

Bonjour, je suis tombé sur ces deux lemmes :

"Soit un espace vectoriel. Si est une famille génératrice de et une famille quelconque de vecteurs de alors la famille est forcément liée."

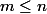
"Soit un espace vectoriel. Si est une famille libre de et que est une famille génératrice de alors et de plus à permutations près, est une famille génératrice de ."

Je me demandais s'il y avait équivalences entre ces deux propositions ?

Merci d'avance !

[aviateur]

Bonjour
La réponse est oui bien sûr. Cela se vérifie facilement.

[Pseuda]

Bonsoir,

Je dirais que non, parce que la 1ère proposition est toujours vraie, et la 2ème pas toujours.

La 1ère : famille génératrice de liée

La 2ème : par exemple en prenant , et (ou ), alors n'est pas une famille génératrice de .

[M.Floquet]

Bonsoir,

Je dirais que non, parce que la 1ère proposition est toujours vraie, et la 2ème pas toujours.

La 1ère : famille génératrice de liée

La 2ème : par exemple en prenant , et (ou ), alors n'est pas une famille génératrice de .

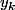
Mais du coup pour le 2ème qu'est-ce qui fait marcher la chose ? Car par construction, on montre que chaque est combinaison linéaire des , puis que l'on peut exprimer en particulier en fonction de et des .

[aviateur]

Exact, je n'ai pas fait attention à la deuxième conclusion du lemme 2.

Effectivement le lemme 2 est faux. Mais par contre si on enlève la partie du lemme 2 "et de plus ...")
alors oui les lemmes 1 et 2 sont équivalents

[M.Floquet]

Exact, je n'ai pas fait attention à la deuxième conclusion du lemme 2.

Effectivement le lemme 2 est faux. Mais par contre si on enlève la partie du lemme 2 "et de plus ...")
alors oui les lemmes 1 et 2 sont équivalents

Ah alors la subtilité vient du "de plus". A ce moment là, si l'on rajoute : "de plus il est possible que" le 2ème énoncé devient valide ?

[Ben314]

Salut,
Peut être signaler quand même que, ce qui est vrai, c'est que :

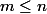
"Soit un espace vectoriel. Si est une famille libre de et que est une famille génératrice de alors et de plus, il existe un entier et tel que la famille soit une base de ."

Que l'on appelle en général le "théorème de la base incomplète".

[Pseuda]

si l'on rajoute : "de plus il est possible que" le 2ème énoncé devient valide ?

Bonjour,

Le 2ème énoncé devient valide si on peut choisir les parmi la famille .

On a : .
Si , est une base donc une famille génératrice.
Sinon (), on choisit (c'est possible, sinon la famille des ne pourrait pas être génératrice de ), et est libre.
Si , est une base donc une famille génératrice.
etc...

C'est le théorème de la base incomplète, en complétant une famille libre avec des vecteurs d'une famille génératrice.