2-1/n<2

[craboulleur]

Bonjour,
Je me creuse la tête depuis 3 jours sur un problème que j'ai rencontré, je cherche à montrer ce qui suit :
En remarquant que pour n appartenant à N* : 2-1/n<2
Montrer que pour tout n appartenant à N* :

1+1/2^2+1/3^2+...+1/n^2<2

je n'arrive pas à partir, dès que j'essaye quelque chose, je n'arrive à rien. Si vous pouvez m'aider, je suis preneur

[aviateur]

Bonjour
Un conseil ne tient pas compte de l'indication 2-1/n<2, c'est du pipeau, même un aveugle peut le voir et ça sert à quoi?
Pour tout il est facile de voir que

d'où
Et puis on fait mieux.
A savoir que la somme vaut

[craboulleur]

Merci pour ta réponse,
Cependant, je ne comprend pas comment tu as trouvé (n-2)/2n

[aviateur]

Cela vient de

D'où

[craboulleur]

merci mais je pense que tu as inversé le (1/2-1/(n-1) avec (1/(n-1)-1/n), ce qui nous donnerait 1+(1-1/2)+(1/2-1/3)+....+(1/(n-1)-1/n)=2-1/n, ce qui nous est donné dans l'énoncé comme cela on peut conclure.
Merci pour ton aide

[Ben314]

Salut,
Tu crois pas quel'indication avec le , elle est pas là pour inciter l'élève à montrer directement (par récurrence et sans astuce concernant la majoration du 1/n^2) que : ?
Ca se fait très bien avec des calculs simples donc ça me semble fort plausible.

[aviateur]

Il faut comprendre ma remarque quand je dis que c'est du pipeau.
D'abord tu as un exercice à résoudre et rien ne t'oblige à suivre l'indication.
Ensuite il y a différents types d'indications, celle qui clairement ouvre la voie vers une démonstration de ce qu'il faut prouver. Parce exemple celle qui t'incite à montrer un résulta intermédiaire (un peu comme si tu ajoutes une question en plus pour faciliter le devoir) ou encore celle qui t'invite à suivre tel type de raisonnement (par l'absurde, par contraposée...)
et puis ce genre d'indication comme ici "remarquer que 2-1/n<2."
Cela veut dire que celui qui a fait l'exercice a suivi une certaine démarche et puis il a utilisé cette (triviale) inégalité , mais cependant ce n'est pas si facile que cela à deviner comment on va utiliser cela. ça complique presque l'exercice.
Evidemment il y a surement une solution qui utilise cette inégalité (d'ailleurs tu le montres) mais je pense
qu'ici et même de façon générale, il vaut mieux essayer de ne pas utiliser toute de suite une béquille qui ne va pas forcément vous aider à marcher mieux. En tout cas c'est comme cela que je vois "les choses".
D'autant plus on s'en passe bien et on montre mieux.

[Ben314]

100% d'accord sur le fait que, vu la forme sous laquelle elle est donné, la soit disant "indication" doit plus ressembler à mystère (voire même à une faute de frappe) pour le lecteur SAUF SI ce dernier sait déjà que l'inégalité demandée peut éventuellement se démontrer par récurrence, mais sûrement pas avec une constante à droite du < (donc ça pourrait répondre à la question "quoi mettre à la place de la constante à droite du <").
Bref, je suis d'accord pour dire que, tel quel,l'énoncé est super mal foutu vu que seul ceux quasi-capable de trouver la solution sans indic. risquent (éventuellement...) de voir à quoi sert l'indication.

Mais ça me semble pas con (y compris si on procède autrement pour faire la preuve) de comprendre pourquoi l'auteur à mis cette indication, non ?

[aviateur]

oui ça oui. bien sûr.
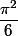
Pour info pour le poseur: la somme vaut exactement mais se démontre avec moyens que surement tu n'as pas encore vu (séries de Fourier par exemple)

[Black Jack]

Salut,

Alternative.

Tracer le graphe de f(x) = 1/x² pour x >= 1 (j'ai tracé jusque x = 4 ... mais évidemment, il faut le prolonger par la pensée).



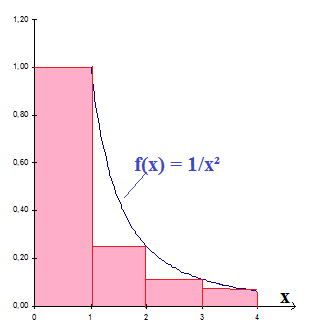
L'aire en rose (sur le graphe prolongé jusque x = n), correspond à 1 + 1/2² + 1/3² + ... + 1/n²

On remarquera que le graphe de f(x) est partout au dessus ou coincide avec l'aire en rose...

Et donc on a







Et comme l'énoncé précise que 2 - 1/n < 2 (mais n'était-ce pas évident ?) , on a donc :

[aviateur]

Oui ok pour l'alternative utile.