Bonjour à tous,
Voici mon exercice:
Une urne contient 2 boules blanches et n − 2 boules rouges.
On effectue des tirages sans remise dans cette urne. On appelle X le rang de sortie de la première boule
blanche et Y le nombre de boules rouges restant à ce moment dans l’urne.
Déterminer la loi de X et E(X).
Pour répondre à la question, je me dis si la boule blanche arrive au premier tirage, donc P(X=1) =2/n, maintenant si la boule blanche arrive au kème tirage,
(X=k) = les k-1 tirages sont sans remise sont rouges et le kème est blanc.
Ce qui me donne ,
P(X=k) = (n-2)/n * (n-3)/(n-1)*...*(n-2-(k-1-1))/(n-(k-1-1))*2/(n-(k-1))
J'ai un souci de calcul, comment arriver au résultat, car j'aurai tendance à faire bêtement:
P(X=k) = (n-2-k+1+1)/(n-k+2) * 2/ (n-k+1) = 2* (n-k) / ((n-k+2) *(n-k+1))
Je vous remercie par avance.
Variable aléatoire
3 messages
- Page 1 sur 1
Re: Variable aléatoire
Bonjour
Je n'arrive pas à bien lire tes calculs bien que tu sembles raisonner correctement
Vérifie tes calculs car je je trouve :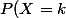= \frac{2 (-k+n)}{(-1+n) n}) et je suis assez sûr de moi car la somme des proba est 1.
et je suis assez sûr de moi car la somme des proba est 1.
Je n'arrive pas à bien lire tes calculs bien que tu sembles raisonner correctement
Vérifie tes calculs car je je trouve :
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
