Dérivées
37 messages
- Page 2 sur 2 - 1, 2
Re: dérivées
Écris avec les détailles comment tu trouves l'équation de la tangente pour le petit 1 de l'exo 2
Re: dérivées
f(x) = x²+3
f(1) = 4
f'(x) = x
f'(1) = 1
T = f'(a) (x-a) + f(a)
= f'(1) (x-1) + f(1)
= 1 (x-1) + 4
= x-1 + 4
f(1) = 4
f'(x) = x
f'(1) = 1
T = f'(a) (x-a) + f(a)
= f'(1) (x-1) + f(1)
= 1 (x-1) + 4
= x-1 + 4
Re: dérivées
Premièrement la dérivé de x² c'est 2x et pas x. Et deuxièmement prend l'habitude de toujours simplifier tes calculs x-1+4=x+3 c'est mieux.
Re: dérivées
mince le boulet désolé je reprend
f(x) = x²+3
f(1) = 4
f'(x) = 2x
f'(1) = 2
T = f'(a) (x-a) + f(a)
= f'(1) (x-1) + f(1)
= 2 (x-1) + 4
= 2x-2 + 4
= 2x + 2
f(x) = x²+3
f(1) = 4
f'(x) = 2x
f'(1) = 2
T = f'(a) (x-a) + f(a)
= f'(1) (x-1) + f(1)
= 2 (x-1) + 4
= 2x-2 + 4
= 2x + 2
Re: dérivées
Ok maintenant je suis d'accord.
Pour la question 2).
Si tu as deux fonctions (f et g par exemple et on note et
et 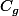 leurs courbes représentatives dans un repère) et qu'on te demande d'étudier les positions relatives de
leurs courbes représentatives dans un repère) et qu'on te demande d'étudier les positions relatives de  et
et 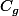 , tu dois en gros dire quand est-ce que la courbe de la fonction f (
, tu dois en gros dire quand est-ce que la courbe de la fonction f ( ) est au dessus de la courbe de la fonction g (
) est au dessus de la courbe de la fonction g (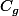 ) et inversement quand est-ce qu'elle est en dessous.
) et inversement quand est-ce qu'elle est en dessous.
Donc tu dois résoudre les inégalités:
(1)\geq g(x))
(2)\leq g(x))
Pour la question 2).
Si tu as deux fonctions (f et g par exemple et on note
Donc tu dois résoudre les inégalités:
(1)
(2)
Re: dérivées
daccord j'essaierais de faire ca!
puisque je manque de temps est ce que tu pourrais commencer a m'expliquer comment m'y prendre pour le 3 A 1) pendant que je planche sur le 2 stp?
puisque je manque de temps est ce que tu pourrais commencer a m'expliquer comment m'y prendre pour le 3 A 1) pendant que je planche sur le 2 stp?
Re: dérivées
Si je t'explique comment faire toutes les questions ça n'a pas un grand intérêt pour toi, surtout si tu n'as pas réfléchis par toi même avant.
Tout d'abord essaye de trouver par toi même, si tu n'arrives pas relis ton cours sur l'exercice en question (dérivée, polynôme, fraction ...) puis réessaye la question. Et après avoir fait ça si tu n'y arrives toujours pas on t'aideras.
Tout d'abord essaye de trouver par toi même, si tu n'arrives pas relis ton cours sur l'exercice en question (dérivée, polynôme, fraction ...) puis réessaye la question. Et après avoir fait ça si tu n'y arrives toujours pas on t'aideras.
Re: dérivées
le truc c'est que je connais mon cours sur les trinomes mais la oon ne nous demande pas d'etudier les signes de h mais quel est le signe de h... hors comme delta et superieur a 0 la representation graphique de h admet 2 racines a l'origine... et comme a est positif les signes seront donc + (x1) - (x2) +
mais ca ne me donne pas le signe de H?
j'ai deja cherché et je ne trouve pas mieux...
mais ca ne me donne pas le signe de H?
j'ai deja cherché et je ne trouve pas mieux...
Re: dérivées
Mahe a écrit:le truc c'est que je connais mon cours sur les trinomes mais la oon ne nous demande pas d'etudier les signes de h mais quel est le signe de h... hors comme delta et superieur a 0 la representation graphique de h admet 2 racines a l'origine... et comme a est positif les signes seront donc + (x1) - (x2) +
mais ca ne me donne pas le signe de H?
j'ai deja cherché et je ne trouve pas mieux...
Oui effectivement la question est peut être mal posé mais c'est normal que le signe change, h n'est pas de signe constant comme delta>0 comme tu l'as dit.
Et oui c'est exactement ça la réponse, reste à calculer x1 et x2.
Re: dérivées
ok merci dans ce cas!
sinon pour le petit 2 je ne comprend pas l'énnoncé : que signifie R \ {-1} ?
sinon pour le petit 2 je ne comprend pas l'énnoncé : que signifie R \ {-1} ?
Re: dérivées
"R\ {-1}" ça veut dire que l'on considère l'ensemble des nombres réels sauf -1.
Et on étudie donc la fonction sur "R\ {-1} car on a une division par x+1 et comme on a pas le droit de diviser par 0 alors forcément x dois être différent de -1.
Et on étudie donc la fonction sur "R\ {-1} car on a une division par x+1 et comme on a pas le droit de diviser par 0 alors forcément x dois être différent de -1.
Re: dérivées
ok merci beaucoup!
ah oui pour le B javais deja essayé un truc pas tres concluant... je te developpe mon calcul dans le message suivant
ah oui pour le B javais deja essayé un truc pas tres concluant... je te developpe mon calcul dans le message suivant
Re: dérivées
f(x) = 2x-5-(3x/ (x+1) )
f'(x) = 2 -- 3x*1}{(x+1)^{2}})
= 2 - ( (3x+3 - 3x) / (x+1)² )
= 2 - (3 / (x+1)²
donc pas du tout égal a ce qu'il fallait trouver...
f'(x) = 2 -
= 2 - ( (3x+3 - 3x) / (x+1)² )
= 2 - (3 / (x+1)²
donc pas du tout égal a ce qu'il fallait trouver...
Re: dérivées
Mahe a écrit:f(x) = 2x-5-(3x/ (x+1) )
f'(x) = 2 -
= 2 - ( (3x+3 - 3x) / (x+1)² )
= 2 - (3 / (x+1)²
donc pas du tout égal a ce qu'il fallait trouver...
Jusque la tout est juste.
Ce qu'il faut trouver est sous une seule fraction donc pour trouver le bon résultat faudrait peut-être mettre tout au même dénominateur non?
Re: dérivées
Rebonjour
Remarque: si on ne répond pas c'est peut être que l'on fait autre chose.
@infernaleur a bien pris le relais.
pour le 2) de l'ex 2.
Tu as=x^2+3) donc l'équation de la tgte
donc l'équation de la tgte  à la courbe
à la courbe  en x=1 est :
en x=1 est :
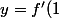*(x-1)+f(1)=2*(x-1)+4=2 x+2.)
Comme est une parabole tournée vers le haut (elle est convexe)
est une parabole tournée vers le haut (elle est convexe)
alors la tgte est située en dessous de la courbe
est située en dessous de la courbe 
Je rappelle tout de même que tu peux ne pas savoir ce résultat classique et ds ce cas il faut étudier le signe de
f(x)-(2x+2) en cherchant à le factoriser.
Remarque: si on ne répond pas c'est peut être que l'on fait autre chose.
@infernaleur a bien pris le relais.
pour le 2) de l'ex 2.
Tu as
Comme
alors la tgte
Je rappelle tout de même que tu peux ne pas savoir ce résultat classique et ds ce cas il faut étudier le signe de
f(x)-(2x+2) en cherchant à le factoriser.
Re: dérivées
J'ai pas vu la correction de @ infernaleur concernant la dérivée (ex 2,1) donc tant pis pour la répétition. OK
37 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
