Dérivées
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 18:43
par Mahe » 19 Aoû 2018, 18:43
Bonsoir,
j'ai un dm de revision sur les dérivées sur lequel je bloque et j'epere que vous pourrez m'aider!
voici le sujet : (cliquer pour agrandir)

alors voila je connais mes dérivées mais je bloque juste sur la maniere d'aborder le premier exercice... pourriez vous me mettre sur la piste?
pour le petit 2 du 2e je ne vois pas du tout

et pour le 3e je n'ai pas encore regardé, je reviendrais vers vous si besoin!
merci d'avance!
-
aviateur
 par aviateur » 19 Aoû 2018, 18:51
par aviateur » 19 Aoû 2018, 18:51
Bonjour
tu dis "Je connais mes dérivées" mais qu'est ce que cela veut dire??
En effet la première question c'est de lire sur le dessin où la dérivée est nulle.
Donc la question c'est pour toi "la dérivée d'une fonction f en un nombre a (i.e f'(a)) cela correspond à quoi graphiquement"? Peux tu répondre à cette question?
-
aviateur
 par aviateur » 19 Aoû 2018, 18:55
par aviateur » 19 Aoû 2018, 18:55
Il faudra aussi pour le deuxième exercice, puisque tu bloques sur la question 2, dire combien tu trouve au 1).
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 19:00
par Mahe » 19 Aoû 2018, 19:00
la dérivée s'annule quand la tangente est horizontale c'est ca?
donc on aurait environ -0,3 ; 2,2 ; 4,6 ?
ca me parait bizarre qu'on ait des valeur approchées non? je dois surement me tromper dans ce cas ^^
-
aviateur
 par aviateur » 19 Aoû 2018, 19:04
par aviateur » 19 Aoû 2018, 19:04
Oui, c'est ça. Il n'y a rien de bizarre. C'est une lecture graphique donc il faut lire au mieux et ceux sont bien des valeurs approchées.
Donne tes réponses pour la suite.
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 19:06
par Mahe » 19 Aoû 2018, 19:06
alors pour le petit 1 du 2 j'ai trouvé pour la tangente : f'(1) (x-1) + f(1) = 1 (x-1) + 4
ca te parait correct?
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 19:08
par Mahe » 19 Aoû 2018, 19:08
daccord merci pour ta réponse!
je vais essayer de faire la suite mais pour l'instant je n'ai franchement pas d'idées... je réfléchis un peu a ca et reviens vers toi plus tard!
Encore merci !
-
aviateur
 par aviateur » 19 Aoû 2018, 19:08
par aviateur » 19 Aoû 2018, 19:08
Oui c'est ça (exercice 2 petit 1) mais simplifie.
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 19:12
par Mahe » 19 Aoû 2018, 19:12
x-1+4?
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 19:22
par Mahe » 19 Aoû 2018, 19:22
donc comme annoncé précédemment je n'ai vraiment pas d'idée pour la suite...
comme on dit qui ne tente rien n'a rien donc je me dis que si la derivée d'un point vaut 0 quand le coefficient directeur de la tangente vaut 0 alors si le coefficient est -4/1 (comme ici) la dérivée du point sera le meme?
je n'aime vraiment pas inventer des theories que je n'ai pas apprise donc je ne suis pas sur mais f'(-1) est il égal a -4/1? (ne te moque pas stp :p)
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 19:25
par Mahe » 19 Aoû 2018, 19:25
j'ai donc fait une petite recherche apres ce commentaire et j'ai l'impression que ce que j'ai dit n'est pas si bete que ce que je pensais

dis moi si j'ai tord...
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 19:34
par Mahe » 19 Aoû 2018, 19:34
pour le petit 3 pour faire le tableau de signes il faut mettre les nombre qu'on a trouvés dans le petit 1, mais je ne sais pas comment justifier les signes a mettre entre chaque "0" du tableau...
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 19 Aoû 2018, 19:46
par infernaleur » 19 Aoû 2018, 19:46
Salut,
l'équation de la tangente d'une courbe au point d'abscisse

est de la forme
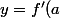(x-a)+f(a))
. Donc oui effectivement le coefficient directeur de la tangente au point d'abscisse

c'est
)
.
Ainsi pour trouver
)
il faut trouver le coefficient directeur de la tangente qui est représenté graphiquement, et pour faire ça tu prend deux points qui appartiennent à la tangente, par exemple le point de coordonné (0,-4) et le point de coordonné (-1,0).
Tu as donc
=\frac{-4-0}{0-(-1)}=-4)
donc oui tu as juste.
Ensuite pour le tableau de signe de la dérivée tu peux utiliser que si une fonction est croissante alors la dérivée est positive et inversement si une fonction est décroissante alors la dérivée est négative.
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 19:54
par Mahe » 19 Aoû 2018, 19:54
merci de ton aide!
pourrais tu juste m'aider a trouver un moyen de justifier tout ce que tu m'as dit dans les 2 premieres phrases de ton message?
merci egalement pour le tableau de signe... alors du coup j'obtiens (entre chaque nombre ou la derrivée s'annule) - ( -0,3) + (2,2) - (4,6) +
c'est ca?
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 20:08
par Mahe » 19 Aoû 2018, 20:08
et pour le petit 4 je trouve -4x
correct?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 19 Aoû 2018, 20:12
par infernaleur » 19 Aoû 2018, 20:12
Pour le tableau de signe c'est juste mais pour l'expression de la tangente T c'est faux. Tu peux détailler comment tu trouves tes résultats ça nous permet de voir où est-ce que tu as fait ton erreur.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 19 Aoû 2018, 20:17
par infernaleur » 19 Aoû 2018, 20:17

c'est la forme d'une fonction linéaire donc qui passe par l'origine, est-ce le cas pour T ?
Un petit rappel : une fonction affine est une fonction de la forme
=ax+b)
où a est le coefficient directeur et b l'ordonné a l'origine (b c'est donc f(0) en fait).
Donc, pour T comme le coefficient directeur c'est -4 et l’ordonné a l'origine c'est -4 aussi tu as directement que l'expression de T est
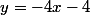
Tu trouves évidemment le même résultat en utilisant la formule
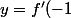(x-(-1))+f(-1).)
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 20:18
par Mahe » 19 Aoû 2018, 20:18
pas de souci alors je suis parti de la formule de la tangente f'(a) (x-a) + f(a)
jai remplacé f'(-1) (x- (-1)) +f(-1)
= -4 (x +1) + 0
= -4x
et je me rend compte en ecrivant que j'ai oublié un -4
donc -4x - 4 c'est mieux?
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 20:19
par Mahe » 19 Aoû 2018, 20:19
merci !
-
Mahe
- Membre Naturel
- Messages: 80
- Enregistré le: 23 Jan 2017, 21:42
-
 par Mahe » 19 Aoû 2018, 20:20
par Mahe » 19 Aoû 2018, 20:20
est ce que je peux te demander ton aide pour le petit 2 du 2e exercice maintenant? O:)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités

