Exercice Trigonometrie
25 messages
- Page 1 sur 2 - 1, 2
Exercice Trigonometrie
Bonjour,
Svp j'ai un exercice à résoudre, si vous avez des solutions. merci
https://s22.postimg.cc/ooj7v4nn5/IMG-7261.jpg
Svp j'ai un exercice à résoudre, si vous avez des solutions. merci
https://s22.postimg.cc/ooj7v4nn5/IMG-7261.jpg
Re: Exercice Trigonometrie
Bonjour
Je ne vais pas faire une réponse complète, ne serait-ce que par je ne suis pas sûr de bien lire le dessin (Surtout au niveau des épaisseurs).
Cependant si tu prends le triangle "intérieur" à gauche. Il est rectangle et à mon avis, grâce aux indications on doit pouvoir donner la mesure des 2 côtés qui forment l'angle droit.
Je les appelle a et b. Alors le troisième côté tu l'as grâce à Phythagore:
En principe tu dois retrouver x en ajoutant les épaisseurs à c.
Maintenant tu as=a/b) (si j'appelle a le côté opposé à
(si j'appelle a le côté opposé à  )
)
Donc)
Evidemment d'un point de vue pratique il faudra aussi utiliser une calculatrice
Je ne vais pas faire une réponse complète, ne serait-ce que par je ne suis pas sûr de bien lire le dessin (Surtout au niveau des épaisseurs).
Cependant si tu prends le triangle "intérieur" à gauche. Il est rectangle et à mon avis, grâce aux indications on doit pouvoir donner la mesure des 2 côtés qui forment l'angle droit.
Je les appelle a et b. Alors le troisième côté tu l'as grâce à Phythagore:
En principe tu dois retrouver x en ajoutant les épaisseurs à c.
Maintenant tu as
Donc
Evidemment d'un point de vue pratique il faudra aussi utiliser une calculatrice
Re: Exercice Trigonometrie
Bonjour, et merci pour votre réponse,
mais je n'ai pas vraiment compris, comment déterminer les a et b
le prof nous a donner comme solution pour les deux figures
Thêta = 30,84° / x=168
Thêta = 37,67° / x=182
mais je n'ai pas vraiment compris, comment déterminer les a et b
le prof nous a donner comme solution pour les deux figures
Thêta = 30,84° / x=168
Thêta = 37,67° / x=182
Re: Exercice Trigonometrie
C'est bizarre car avec ce résultat on retrouve comme hauteur
144 tan(30.84°)=85.97 cm=86cm
La différence qui manquait est donc 86cm-72 cm=14 cm.
Or cette différence devrait être = à
12/sin(30.84°)=23.40 cm.
Soit l'enseignant s'est trompé ou alors il fait des approximations.
Là je ne peux pas en dire plus à cause du manque de précision de l'énoncé.
144 tan(30.84°)=85.97 cm=86cm
La différence qui manquait est donc 86cm-72 cm=14 cm.
Or cette différence devrait être = à
12/sin(30.84°)=23.40 cm.
Soit l'enseignant s'est trompé ou alors il fait des approximations.
Là je ne peux pas en dire plus à cause du manque de précision de l'énoncé.
Re: Exercice Trigonometrie
Merci beaucoup, je vais discuté avec le prof, s il a plus de precision pour cet exercice.
Re: Exercice Trigonometrie
Bonjour,
je viens d'avoir de l'enseignant une image plus claire de l'exercice posté, j’espère que vous allez pourvoir m'aider à le résoudre.
merci beaucoup

je viens d'avoir de l'enseignant une image plus claire de l'exercice posté, j’espère que vous allez pourvoir m'aider à le résoudre.
merci beaucoup

Re: Exercice Trigonometrie
Bonjour
Effectivement on voit bien mieux. Mais par rapport à la solution que tu donnes, je ne trouve pas le même.
Mais ce n'est pas aussi éloigné.
Je t'explique comment je fais et tu pourras vérifier si tu veux. (Nota: pour simplifier je pose,)
) et
et )
Le petit problème c'est que je ne peux pas refaire la figure.
Donc je pars d'un triangle rectangle: (celui obtenu en coupant la figure en deux mais j'ai enlevé l'épaisseur du bas.
Un angle de ce triangle vaut , l'hypoténuse vaut x , le côté adjacent vaut 144, le côté opposé
, l'hypoténuse vaut x , le côté adjacent vaut 144, le côté opposé
72 +2 w.
J'espère que tu vois le triangle)
w c'est quoi: la demi longueur de la diagonale verticale du petit losange dont un cote mesure 12. Faire un dessin, placer dans ce losange pour voir que
dans ce losange pour voir que
s=w/12.
Il vient donc/144=1/2+s/6=s/c=s/(\sqrt{1-s^2).)
Voici mon équation. Le reste n'est qu'un calcul faire précision.
) conduit à
conduit à 
D'où=0.528614 radian=30.2873) degré (on ne trouve pas le m^me !!)
degré (on ne trouve pas le m^me !!)
et idem
idem
Effectivement on voit bien mieux. Mais par rapport à la solution que tu donnes, je ne trouve pas le même.
Mais ce n'est pas aussi éloigné.
Je t'explique comment je fais et tu pourras vérifier si tu veux. (Nota: pour simplifier je pose
Le petit problème c'est que je ne peux pas refaire la figure.
Donc je pars d'un triangle rectangle: (celui obtenu en coupant la figure en deux mais j'ai enlevé l'épaisseur du bas.
Un angle de ce triangle vaut
72 +2 w.
J'espère que tu vois le triangle)
w c'est quoi: la demi longueur de la diagonale verticale du petit losange dont un cote mesure 12. Faire un dessin, placer
s=w/12.
Il vient donc
Voici mon équation. Le reste n'est qu'un calcul faire précision.
D'où
et
Re: Exercice Trigonometrie
Bon j'ai vérifié. En fait il faut faire comme j'ai dit car je suis assez convaincu que ton prof a fait comme moi
à la différence près (sauf erreur de ma part):
J'ai résolu l'équation non linéaire d'inconnue s avec une précision de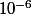 . Il se peut que ton prof a résolu cette "équation (ou une équivalente) avec une précision moindre ce qui engendre un léger écart sur la valeur de
. Il se peut que ton prof a résolu cette "équation (ou une équivalente) avec une précision moindre ce qui engendre un léger écart sur la valeur de  trouvée par chacun. Ensuite l'erreur pour x est automatiquement amplifiée de
trouvée par chacun. Ensuite l'erreur pour x est automatiquement amplifiée de
1 cm environ et ton prof a surement encore arrondi au cm le plus proche. Mais l'erreur (j'entends par là la différence de résultats) est cohérente par rapport à son approximation.
C'est à dire qu'il n'y pas de problème mathématique au sens propre du terme.
Le tout est de savoir par rapport aux mesures qu'elles sont les marges d'erreurs acceptables mais ce n'est pas explicitement la question. En résumé les deux résultats sont bons et ne sont pas incompatibles d'après moi.
à la différence près (sauf erreur de ma part):
J'ai résolu l'équation non linéaire d'inconnue s avec une précision de
1 cm environ et ton prof a surement encore arrondi au cm le plus proche. Mais l'erreur (j'entends par là la différence de résultats) est cohérente par rapport à son approximation.
C'est à dire qu'il n'y pas de problème mathématique au sens propre du terme.
Le tout est de savoir par rapport aux mesures qu'elles sont les marges d'erreurs acceptables mais ce n'est pas explicitement la question. En résumé les deux résultats sont bons et ne sont pas incompatibles d'après moi.
Re: Exercice Trigonometrie
Bonjour, BRAVO !!! j’apprécie ton soutien et je te remercie pour le temps consacré à résoudre l'exercice,
je suis rendue à cette formule, , j'ai remplacée sin(thêta) par x, après factorisation et tout j'ai eu la fonction du 4eme degré suivante x4+6x3+44x2-6x-9=0 je n'ai pas arrivée à trouver des racines pour la résoudre, j'ai utilisée juste une site en ligne et j'ai reçue le même résultat que tu m'a donné. y a pas une méthode plus simple pour la résoudre ?
, j'ai remplacée sin(thêta) par x, après factorisation et tout j'ai eu la fonction du 4eme degré suivante x4+6x3+44x2-6x-9=0 je n'ai pas arrivée à trouver des racines pour la résoudre, j'ai utilisée juste une site en ligne et j'ai reçue le même résultat que tu m'a donné. y a pas une méthode plus simple pour la résoudre ?
merci beaucoup
je suis rendue à cette formule,
 , j'ai remplacée sin(thêta) par x, après factorisation et tout j'ai eu la fonction du 4eme degré suivante x4+6x3+44x2-6x-9=0 je n'ai pas arrivée à trouver des racines pour la résoudre, j'ai utilisée juste une site en ligne et j'ai reçue le même résultat que tu m'a donné. y a pas une méthode plus simple pour la résoudre ?
, j'ai remplacée sin(thêta) par x, après factorisation et tout j'ai eu la fonction du 4eme degré suivante x4+6x3+44x2-6x-9=0 je n'ai pas arrivée à trouver des racines pour la résoudre, j'ai utilisée juste une site en ligne et j'ai reçue le même résultat que tu m'a donné. y a pas une méthode plus simple pour la résoudre ?merci beaucoup
Re: Exercice Trigonometrie
le tracé à l'échelle (et on voit que c'est l'épaisseur 12 qui gène pour le tracé), j'ai pour 72 , x= 168.
ce qui me force à vérifier par calcul
[édit inutile] 167.7 par calcul.
la hauteur de l’arbalétrier de 12 vu dans le sens de la hauteur est : (1+2*sqrt(179))*72/143 = 13.97...
et par Pythagore x= 167.7137...
Conclusion : un dessin à l'échelle dans la vraie vie, y a que ça de vrai
ce qui me force à vérifier par calcul
[édit inutile] 167.7 par calcul.
la hauteur de l’arbalétrier de 12 vu dans le sens de la hauteur est : (1+2*sqrt(179))*72/143 = 13.97...
et par Pythagore x= 167.7137...
Conclusion : un dessin à l'échelle dans la vraie vie, y a que ça de vrai
Modifié en dernier par pascal16 le 24 Aoû 2018, 09:07, modifié 3 fois.
Re: Exercice Trigonometrie
Salut,
Je suis pas certain d'avoir bien compris comment tu avais mené tes calculs.
Perso, pour h=72, je trouve un angle de 30,83959059 (en degré) et x=167,7137367.
Si ça semble plus plausible, je mettrais la méthode que j'ai employée.
Mais de toute façon, sur la figure, c'est pas archi. clair de comprendre où s'arrête le bord gauche de la mesure du x.
J'ai considéré que c'était dans le prolongement de la droite formée par le haut du chevron du bas (à l'horizontale).
Je suis pas certain d'avoir bien compris comment tu avais mené tes calculs.
Perso, pour h=72, je trouve un angle de 30,83959059 (en degré) et x=167,7137367.
Si ça semble plus plausible, je mettrais la méthode que j'ai employée.
Mais de toute façon, sur la figure, c'est pas archi. clair de comprendre où s'arrête le bord gauche de la mesure du x.
J'ai considéré que c'était dans le prolongement de la droite formée par le haut du chevron du bas (à l'horizontale).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Exercice Trigonometrie
Je me sert de proportionnalité entre 12, 288/2 et une des dimensions recherchée pour l'équation
pour 96, graphiquement, x=182
la hauteur de 12 vue sur la hauteur est la solution positive de h²(1-1/144)-4/3 h-208=0
(ou la racine positive de h²(1-1/144)-4/3 h-208 pour certains...)
et finalement x= 181.9.....
pour 96, graphiquement, x=182
la hauteur de 12 vue sur la hauteur est la solution positive de h²(1-1/144)-4/3 h-208=0
(ou la racine positive de h²(1-1/144)-4/3 h-208 pour certains...)
et finalement x= 181.9.....
Re: Exercice Trigonometrie
Bon je réponds un peu à tout le monde.
@ben Du point de vue méthode c'est pas le problème c'est Pythagore ou bien de la trigo.
Pour avoir des résultats un peu différents cela vient
1. d'une part de la figure. Perso, ici avec les nouvelles figures j'ai considéré que le petit morceau au dessus de la côte 72 cm est un (petit) losange. Il dc faut ajouter la diagonale verticale de ce losange qui se calcule exactement. A mon avis c'est la lecture la plus précise. Le prix à payer c'est que l'on se retrouve avec une équation non linéaire (qui peut se ramener aussi à une équation polynomiale de degré 4).
2. La résolution numérique de cette équation peut être faite avec + ou moins de précision, cette différence de précision amplifie les différences de résultats des uns des autres.
Maintenant je suppose que tu fais une lecture un peu différente des mesures du dessin. C'est bien cela? comme tu sembles approcher mieux les résultats du prof, tu peux expliquer en deux mots, cela peut intéresser @Ouumsara.
Maintenant @Ouumsara. Si on procède comme cela on se retrouve avec une équation d'inconnue s, non linéaire insolvable (ou difficilement solvable)exactement.
Evidemment comme tu l'as fait l'équation est équivalente à résoudre un polynôme de degré 4 (solvable mais de façon compliquée) et alors on cherche la solution numériquement par une méthode (numérique).
Chacun fait comme il veut mais la méthode la plus adaptée est la méthode de Newton.
Donc il n'y a pas plus simple sauf si on lit la figure un peu différemment où je ne sais pas quoi?
(Voir les autres réponses ici).
@ben Du point de vue méthode c'est pas le problème c'est Pythagore ou bien de la trigo.
Pour avoir des résultats un peu différents cela vient
1. d'une part de la figure. Perso, ici avec les nouvelles figures j'ai considéré que le petit morceau au dessus de la côte 72 cm est un (petit) losange. Il dc faut ajouter la diagonale verticale de ce losange qui se calcule exactement. A mon avis c'est la lecture la plus précise. Le prix à payer c'est que l'on se retrouve avec une équation non linéaire (qui peut se ramener aussi à une équation polynomiale de degré 4).
2. La résolution numérique de cette équation peut être faite avec + ou moins de précision, cette différence de précision amplifie les différences de résultats des uns des autres.
Maintenant je suppose que tu fais une lecture un peu différente des mesures du dessin. C'est bien cela? comme tu sembles approcher mieux les résultats du prof, tu peux expliquer en deux mots, cela peut intéresser @Ouumsara.
Maintenant @Ouumsara. Si on procède comme cela on se retrouve avec une équation d'inconnue s, non linéaire insolvable (ou difficilement solvable)exactement.
Evidemment comme tu l'as fait l'équation est équivalente à résoudre un polynôme de degré 4 (solvable mais de façon compliquée) et alors on cherche la solution numériquement par une méthode (numérique).
Chacun fait comme il veut mais la méthode la plus adaptée est la méthode de Newton.
Donc il n'y a pas plus simple sauf si on lit la figure un peu différemment où je ne sais pas quoi?
(Voir les autres réponses ici).
Re: Exercice Trigonometrie
Bonjour
Je reviens sur ta question concernant le polynôme de degré 4. Pour un polynôme de degré 3 ou 4 on sait trouver exactement ses racines mais (sauf par chance) en général les formules sont très compliqués et le calcul est long.
On préfère une méthode numérique comme la méthode de Newton par exemple.
Désignons par P le polynôme tel que l'on cherche une racine s (réelle ici) (i.e P(s)=0)
On choisit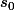 assez proche de s. (ici s est un sinus on peut commencer par
assez proche de s. (ici s est un sinus on peut commencer par  )
)
En suite on pose/P'(s_{n-1}),n=1,2,3) et (bien sûr après une certaine analyse pour être sûr que ça marche) la suite
et (bien sûr après une certaine analyse pour être sûr que ça marche) la suite 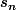 converge vers s. Mais la convergence est très (très) rapide avec Newton (s_3,s_4 donnent des valeurs très proche de s).
converge vers s. Mais la convergence est très (très) rapide avec Newton (s_3,s_4 donnent des valeurs très proche de s).
Je reviens sur ta question concernant le polynôme de degré 4. Pour un polynôme de degré 3 ou 4 on sait trouver exactement ses racines mais (sauf par chance) en général les formules sont très compliqués et le calcul est long.
On préfère une méthode numérique comme la méthode de Newton par exemple.
Désignons par P le polynôme tel que l'on cherche une racine s (réelle ici) (i.e P(s)=0)
On choisit
En suite on pose
Re: Exercice Trigonometrie
aviateur a écrit:....s j'ai considéré que le petit morceau au dessus de la côte 72 cm est un (petit) losange. Il dc faut ajouter la diagonale verticale de ce losange qui se calcule exactement.
la partie en diagonale s'appelle l'arbalétrier
le bois horizontal est le tirant
le bois à a verticale le poinçon il me semble
la hauteur de l’arbalétrier de 12 vu dans le sens de la hauteur est : (1+2*sqrt(179))*72/143 = 13.97...
c'est à dire la demi-diagonale dans le sens du losange vaut13.97
Re: Exercice Trigonometrie
Salut,
Dans le triangle de hauteur 72 de gauche :
base = 288/2 - 12/sin(theta)
h = 72
72 = (288/2 - 12/sin(theta))*tg(theta)
72 = (144 - 12/sin(theta))*tg(theta)
6 = (12 - 1/sin(theta))*tg(theta)
6 = 12.tg(theta) - 1/cos(theta)
1/cos(theta) = 12.tg(theta) - 6 (1)
1/cos²(theta) = 144.tg²(theta) + 36 - 144.tg(theta) (attention l'élévation au carré peut générer des solutions parasites, il faudra donc les vérifier en fin de calcul)
1 + tg²(theta) = 144.tg²(theta) + 36 - 144.tg(theta)
143.tg²(theta) - 144.tg(theta) + 35 = 0
tg(theta) = 0,597056560561 ou 0,409936446462
theta = 30,84° ou 24,898°
En remettant ces valeurs dans (1), on vérifie que le seul angle possible est theta = 30,84°
...
Dans le triangle de hauteur 72 de gauche :
base = 288/2 - 12/sin(theta)
h = 72
72 = (288/2 - 12/sin(theta))*tg(theta)
72 = (144 - 12/sin(theta))*tg(theta)
6 = (12 - 1/sin(theta))*tg(theta)
6 = 12.tg(theta) - 1/cos(theta)
1/cos(theta) = 12.tg(theta) - 6 (1)
1/cos²(theta) = 144.tg²(theta) + 36 - 144.tg(theta) (attention l'élévation au carré peut générer des solutions parasites, il faudra donc les vérifier en fin de calcul)
1 + tg²(theta) = 144.tg²(theta) + 36 - 144.tg(theta)
143.tg²(theta) - 144.tg(theta) + 35 = 0
tg(theta) = 0,597056560561 ou 0,409936446462
theta = 30,84° ou 24,898°
En remettant ces valeurs dans (1), on vérifie que le seul angle possible est theta = 30,84°
...
Re: Exercice Trigonometrie

les triangle ABC et DEF sont semblables.
c'est plus facile pour trouver EF
Pythagore donne les longeurs
la trigo sert à trouver l'angle
Re: Exercice Trigonometrie
Bonjour,
merci pour vos interactions, et vos réponses pertinentes,
comment vous voyez cette méthode de résolution ?

merci à vous
merci pour vos interactions, et vos réponses pertinentes,
comment vous voyez cette méthode de résolution ?

merci à vous
Re: Exercice Trigonometrie
Resalut,
Pour le calcul de x (dessin de gauche de l'énoncé)
Pythagore : (72 + 12/cos(theta))²+ 144² = x²
et avec theta = arctg(0,597056560561) = 30,8399726417° (que j'ai arrondi à 30,84° dans ma réponse précédente), on trouve :
x = 167,71373665 cm (à arrondir bien entendu).

Pour le calcul de x (dessin de gauche de l'énoncé)
Pythagore : (72 + 12/cos(theta))²+ 144² = x²
et avec theta = arctg(0,597056560561) = 30,8399726417° (que j'ai arrondi à 30,84° dans ma réponse précédente), on trouve :
x = 167,71373665 cm (à arrondir bien entendu).
Re: Exercice Trigonometrie
(3 plombes pour faire un malheureux dessin...)

La façon dont je vois les chose c'est le dessin ci dessus où
- La droite (AE), c'est le haut du chevron horizontal (qui est en bas)
- La droite (AD) c'est le milieu du chevron vertical (qui est au milieu)
- Les droites (BC) et (DE) c'est le haut et le bas du chevron de gauche en biais
- La hauteur égale à 72 ou 96, c'est AB.
égale à 72 ou 96, c'est AB.
- La longueur cherchée, c'est DE.
cherchée, c'est DE.
Puis, en posant comme toi) et
et ) :
:
- Dans le triangle ECF, on a\!=\!\dfrac{FC}{EC}\!=\!\dfrac{12}{EC}) donc
donc  .
.
- Dans le triangle ABC, on a\!=\!\dfrac{AB}{AC}\!=\!\dfrac{h}{144\!-\!EC}\!=\!\dfrac{h}{144\!-\!\frac{12}{s}}) donc
donc 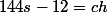 puis
puis \!=\!(144 s)^2\!=\!(ch\!+\!12)^2) qui donne (second degré)
qui donne (second degré) }{h^2+20736})
- Dans le triangle ADE, on a\!=\!\dfrac{AE}{DE}\!=\!\dfrac{144}{x}) donc
donc }{12\sqrt{h^2+20592}-h})

La façon dont je vois les chose c'est le dessin ci dessus où
- La droite (AE), c'est le haut du chevron horizontal (qui est en bas)
- La droite (AD) c'est le milieu du chevron vertical (qui est au milieu)
- Les droites (BC) et (DE) c'est le haut et le bas du chevron de gauche en biais
- La hauteur
- La longueur
Puis, en posant comme toi
- Dans le triangle ECF, on a
- Dans le triangle ABC, on a
- Dans le triangle ADE, on a
Modifié en dernier par Ben314 le 24 Aoû 2018, 20:45, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
