Polynome et fonction polynomiale

[Viko]

Bonjour,

On sait que lorsque est un corps infini et
sont isomorphe en tant que -algèbre.
Je ne vois a priori aucune contre-indication à affaiblir les hypothèses et à énoncer si est un anneau infini et sont isomorphe en tant qu'anneau et en tant que -module pourtant j'ai la bizarre impression de manquer une subtilité, est-ce le cas ?

[Ben314]

Salut,
C'est bien évidement faux dans le cas général d'un anneau commutatif, unitaire mais pas forcément intègre.
Par exemple si I est un ensemble quelconque, l'ensemble P(I) des parties de I est un anneau (commutatif, unitaire) pour la différence symétrique (= '+') et l'intersection (= 'x' ). Or, pour tout A de P(I), on a A²=A donc A²-A=0 ce qui signifie que la fonction associée au polynôme X²-X est identiquement nulle bien que le polynôme soit non nul.

Et sinon, je te dissuade plus que fortement d'écrire un truc du style K[x] pour l'anneau des fonction polynômes : le symbole K[?], c'est systématiquement l'anneau des polynômes formels sur K et ce qu'on met comme ?, ça sert uniquement à donner un nom au polynôme (0,1,0,0,0,0,...) histoire de simplifier les notations.

[Viko]

Oui en effet, mais je me doutais qu'il y avait un contre exemple un peu saugrenue de ce genre....

je viens de comprendre là où ça ne fonctionnait pas dans mon raisonnement, j'utilise le fait que si un polynôme à une infinité de racine il est nul or ce fait est basé sur la formule qui est uniquement valable pour des polynômes à coefficients dans un anneau intègre.

On peut donc énoncer :

Soit un anneau commutatif intègre infini alors en tant qu'anneau et -module (je note l'ensembles des fonctions polynomiales à coefficients dans )

PS : j'ai l'impression qu'on peut se passer du "commutatif" mais je suis pas encore sûr, je crois qu'on en a besoin pour démontrer certaine(s) propriété(s) qui implique(nt) qu'un polynôme avec une infinité de racine est nul je suis entrain d'y jeter un œil....

[Ben314]

1) C'est certes vrai (avec A commutatif, unitaire intègre), mais on peut franchement pas dire que ça apporte du "bien mieux" par rapport au cas d'un corps vu qu'un tel anneau possède un corps des fractions et qu'on peut parfaitement raisonner dans ce corps. Et à mon sens, le résultat archi important, c'est le fait qu'un polynôme de degré n admet au plus n racine. Et le fait que si deux fonction polynôme coïncident (sur A infini) alors les polynômes formels sont égaux, c'est un simple corollaire trivial de cette proposition là.

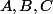
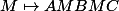
2) Dans le cas non commutatif, ça m’intéresserait de savoir commet tu défini la notion de "fonction polynôme". Par exemple dans l'anneau, A=Mn(K) [matrice nxn à coeff. dans K], si sont des matrices fixées, est-ce que tu considère que est une "fonction polynôme" ou pas ? Et si oui, est-ce qu'il lui correspond à un quelconque polynôme formel de A[X] ?

En bref, la "logique" dans tout ça, c'est que déjà si on considère les polynômes (formels) sur un anneau A, si A n'est pas commutatif, ben faut pas trop espérer les relier a des soit-disant "fonction polynômes" de A dans A. A la limite, on peut leur associer des fonction que vont du "centre" de A (i.e. les élément qui commutent avec tout les autres) dans A.
Ensuite, les résultat archi-classique à connaître (et bien sûr dont il faut absolument connaître les preuves pour savoir dans quel cas ils s'adaptent) c'est dans l'ordre :
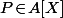
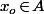
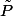
- Si A est commutatif et si est tel que pour un certain (où désigne la fonction polynôme associée à ) alors pour un certain .
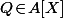
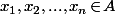
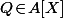
- Si de plus A est intègre, alors, si avec distincts alors pour un certain . Le coté intègre est évidement indispensable si, partant de , on veut déduire que partant de .
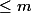
- En particulier, cela prouve que, si A est commutatif et intègre, un polynôme de degré ne peut pas avoir plus de racine et donc que si deux polynômes de degré sont égaux en strictement plus de valeurs, alors ils sont égaux (au sens des polynômes formels bien évidement)
- Et, en particulier de en particulier, cela prouve (toujours avec A est commutatif et intègre), que si deux polynômes sont égaux en une infinité de points alors ils sont égaux (deux polynômes de R[X] prenant les mêmes valeurs sur N ou bien sur {1/n ; n dans N*} sont forcément égaux)


Et pour voir que ça marche pas du tout comme ça dans le cas non commutatif, tu peut aussi regarder simplement le corps de quaternions (qui est bien évidement intègre) où le polynôme X^2+1 admet une infinité de racines.

P.S. Et je dirait pas que l'ensemble P(I) muni de ces deux loi soit "saugrenu" : Z/2Z, c'est évidement un anneau, et même sans doute le plus simple qui soit et P(I) muni des deux lois en question, c'est jamais que l'anneau (Z/2Z)^I donc rien de bien saugrenu.