En théorie des ensembles, on définit les ordinaux comme des ensembles dont chaque élément est également un sous-ensemble.
Pur faire court sans tout développer (c'est un peu long... c'est déjà pas mal long ci-dessous !)
Le plus petit ordinal est l'ensemble vide. On le note "zéro" :
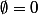
Le second ordinal est l'ensemble dont l'unique élément est l'ensemble vide : on le note "un" :
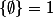
Le troisième ordinal est l'ensemble qui contient deux éléments : zéro et un. On le note 2 :
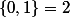
(c'est-à-dire,
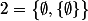
On poursuit ainsi par récurrence : si
est un ordinal, l'ordinal suivant est
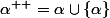
(j'utilise la notation ++ car c'est le symbole pour incrémenter en langage informatique C : "on passe au suivant"...)
La théorie des ensembles énonce alors "l'axiome de l'infini" : il existe un ensemble qui contient zéro et tel que s'il contient
, il contient alors
Avec cet axiome (qui énonce l'existence d'un ensemble, mais il peut y en avoir plusieurs et d'ailleurs il y en a une infinité), on démontre aisément qu'il y en a un "plus petit". Cet ensemble est noté
, mais en fait ce n'est rien d'autre que
(vu qu'on a défini les ordinaux de telle sorte que le premeir est 0, le second est 1, etc.).
Mais alors le principe de construction des ordinaux dit que l'ensemble
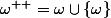
est bien un ordinal, et c'est le premier ordinal après
, lequel est exactement le plus petit ordinal supérieur à tous les entiers naturels : on vient donc de définir
, soit rien autre que
Et évidemment, on ne s'arête pas là : on définit de même
, jusqu'à
et on ne s'arrête pas là évidemment...
On remarque ces deux propriétés :
- tout ordinal a un unique successeur : par construction, c'est
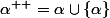
- mais certains ordinaux n'ont pas de prédécesseur : c'est le cas de 0 de façon claire, mais c'est aussi le cas de , de (et en fait de tous les ordinaux obtenus en ajoutant plein de fois à 0). De tels ordinaux infinis sont appelés ordinaux limites.
Ah oui, je suis passé un peu vite sur "l'addition" : on définit l'addition par une relation de récurrence, mais malheureusement, on perd la commutativité dès qu'on dépasse l'infini : ainsi
est le 3ème ordinal après
, mais
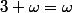
On définit également la mulitplication : ainsi
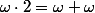
, mais
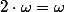
Puis l'exponentiation :
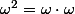
, etc.
On montr même qu'on peut écrire les ordinaux de façon unique "en base
" !
On est obligé de "perdre" la commutativité, car le fait qu'un ordinal limite n'ait pas de prédécesseur force à gérer différemment la relation de récurrence (qu'on appelle "récurrence transfinie")
- dans une récurrence classique (sur des entiers naturels), on définit le point de départ, puis la relation pour passer au suivant
- dans la récurrence transfinie, on ne peut pas se contenter de cela, car on n'atteint jamais ni aucun des ordinaux suivants, vu que n'a pas de prédécesseur. La relation de récurrence transfinie, tout comme le raisonnement par récurrence transfinie, s'effectue alors ainsi
- On définit la situation initiale (pour 0)
- On donne la règle pour passer au suivant comme dans le cas classique
- et pour un ordinal limite, on donne la règle qui permet de passer de l'ensemble des ordinaux inférieurs à l'ordinal limite
Si vous voulez creuser ces aspects, vous pouvez télécharger les documents du site
http://hdci.unblog.fr qui est une forme de cours sur la théorie des ensembles, et qui décrit avec beaucoup de détail la construction des ordinaux (et la hiérarchie impressionnante des infinis...)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
