Bonjour,
Je butte sur le sujet suivant :
Soit n un entier naturel non nul et p compris entre 1 et n. Notons Dp la droite d'équation y = tan((1+p/n)pi/2).x .
Soit M dans le plan réel, Mp son symétrique par rapport à Dp et zp l'affixe de Mp. Montrer que 1/n fois la somme de p = 1 à n-1 des zp converge lorsque n tend vers l'infini.
Le corrigé de mon livre donne directement zp de façon explicite, j'aimerai savoir comment le déterminer.
Déterminer Symétriques
4 messages
- Page 1 sur 1
Re: Déterminer Symétriques
par Ben314 » 23 Juil 2018, 09:21
Salut,
La droite
passe par l'origine 
et fait un angle \frac{\pi}{2})
avec l'axe des 
.
Donc si
a pour affixe 
alors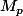 
a pour affixe }\!=\!-\omega_n^p\overline{z}\ \text{ o\`u }\omega_n\!=\!e^{i\frac{\pi}{n}})
et donc }\ \text{ car }\ \omega_n^n\!=\!e^{i\pi}\!=\!-1)
.
\!=\!n\big(1\!-\!\cos\big(\frac{\pi}{n}\big)\big)\!-\!i n\sin\big(\frac{\pi}{n}\big)\mathop{\longrightarrow}\limits_{n\to\infty}0\!-\!i\pi)
.
.
La droite
Donc si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Déterminer Symétriques
par HardcoreLulu99 » 23 Juil 2018, 13:05
Une dernière question, comment trouvez vous l'argument de zp ?
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :