Ensemble non fini d'entier et dénombrabilité

[Viko]

Bonjour,

Comment montrer que toute partie non fini de est de même cardinal que ?

Ma meilleure tentative pour le moment est de construire par récurrence une suite indexée par à valeur dans la dite partie mais cela ne me satisfait pas puisque le raisonnement par récurrence va seulement permettre de construire une suite arbitrairement longue d'élément de la partie sans jamais réussir à en faire une suite non fini d'élément, tout cela manque donc un peu de rigueur... des idées ?

[pascal16]

soit P une partie non finie de N
on tri ses éléments par ordre croissant.
on met en relation le i iéme élément de P ainsi classé avec le nombre i de N.

On a ainsi pris TOUS les éléments de P (c'est le plus dur à démontrer quand on ne part pas d'une partie de N).
Tout élément de P a une image dans N, tout élément de N a un antécédent car sinon P serait fini.
On a donc une bijection de P sur N.

Et que dit la bijection sur la dénombrabilité de P ?

Ca fait toujours bizarre qu'il y ait autant de nombre premiers que de nombres du point de vue de la dénombrabilité.

[Viko]

Et bien la bijection dit que P est dénombrable !

Mais ce qui me chagrine un peu c'est :

n met en relation le i iéme élément de P ainsi classé avec le nombre i de N.

c'est cette idée que j'ai utilisé pour ma récurrence mais je ne la trouve pas assez rigoureuse , n'y a-t-il pas un moyen de rendre cela rigoureux ?

[Pseuda]

Bonjour,

Ce que je ferais. Soit une partie infinie de . On construit une application u : N-> I de cette façon :
u(0)=min I (il existe car .... ?)
u(1)=min I\{u(0)} (il existe car .... ?)
...
u(n)=min I\{u(0), u(1), ... u(n-1)}

A chaque pas, l'ensemble I\{u(0), u(1), ... u(n)} est non vide (sinon I serait fini), et son min existe. Il faut montrer maintenant que cette application est bijective. L'injectivité paraît facile.

[Ritaatira]

Salut,
L'idee qui m'est apparue c'est qu'on sait que si [n,+∞[ est inclus dans N (en considerant que qlqsoit x app a [n,+∞[/x est un entier positif) alors: card[n,+∞[<=cardN.. il suffit de montrer l'egalite des cardinaux. En sachant que 2 ensembles (l'un inclus dans l'autre) ont le meme cardinal s'ils sont en bijections.
En ce cas la .. on peut montrer qu'il existe une bijection de [n,+∞[ dans N qui est explicitee en : x-->x-n
Par exple:
Si n=3 ( on aura [3,+∞[)
3-->0
4-->1
5-->2
Et etc.
Donc .. cardN=card[n,+∞[ (n app a N)

[nodgim]

Par l'absurde aussi, peut être ?
Il est évident que N est assez grand pour numéroter dans l'ordre tout élément de P, partie de N.
A contrario, si un élément de N n'était pas un numéro d'ordre de P, ça signifierait que P est fini.

[hdci]

Ce qu'a écrit Pseuda est correct : on constitue la suite formellement de façon itérative.

Si cela ne paraît pas "suffisamment rigoureux", c'est qu'on utilise implicitement un théorème de la théorie des ensembles qui affirme l'existence et l'unicité d'une suite définie par une relation de récurrence : en voici l'énoncé dans le cas simple (non paramétré, récurrence simple)

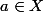
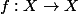
Soit un ensemble, et une fonction dans .
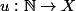
Alors il existe une unique fonction telle que et

[ La démonstration de ce théorème est simple, on distingue existence et unicité, et dans les deux cas on raisonne par l'absurde en utilisant le fait que toute partie de admet un plus petit élément qui a un prédécesseur s'il n'est pas nul (s'il existe des pour lesquels la fonction n'est pas définie, soit le plus petit de ces , il est plus grand que 0 donc admet un prédécesseur pour qui la fonction est définie et par suite la relation donne la valeur de , contradiciton...) ]

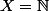
Dans le cas présent, et est définie comme : le théorème précédent affirme l'existence et l'unicité de la suite (reste à justifier que est bien défini pour tout entier, mais ce n'est pas trop difficile)

Il n'y a plus qu'à vérifier que c'est une bijection entre et et ce n'est pas très difficile.

[Viko]

@hdci c'est ce genre d'argument que je cherchais !

[hdci]